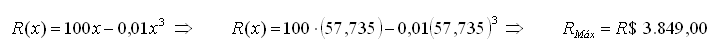Exercício resolvido 1

Um empresário produz e vende certo produto, cujo custo de fabricação é dado por . A demanda para esse produto obedece à relação . Qual o preço que deve ser cobrado para que o lucro seja máximo?

1º) Como se quer maximiza o lucro, deve-se então, primeiramente, determinar a função lucro.

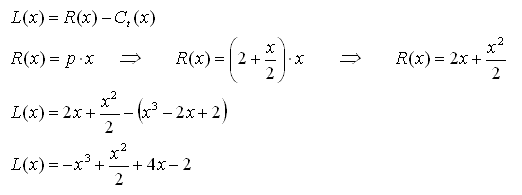
2º) Vamos determinar os pontos críticos.

Resolvendo a equação , tem-se , cujas raízes são dadas por: e .

3º) Aplicar o teste da 2ª derivada para determinar qual ponto é de máximo.

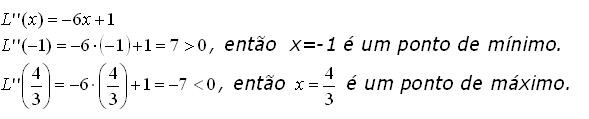
4º) Determinar o preço para o qual o Lucro é máximo

Para encontrar o valor do lucro máximo é só substituir , que é a abscissa correspondente ao ponto de máximo, na função lucro. Logo,

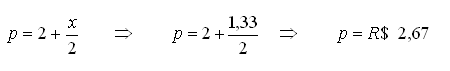
Exercício resolvido 2

2) Seja a função Custo Total dada por . Determinar a quantidade que deve ser produzida para que o custo seja mínimo e o seu valor correspondente.

1º) Vamos determinar os pontos críticos para a função custo.

Resolvendo a equação , tem-se , cujas raízes são dadas por: e .

2º) Aplicar o teste da 2ª derivada para determinar qual ponto é de mínimo.

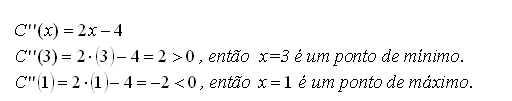
Dessa forma, é a quantidade que deve ser produzida para que o custo seja mínimo.

3º) Determinar o valor do custo mínimo.

Para encontrar o valor do custo mínimo é só substituir , que é a abscissa correspondente ao ponto de mínimo, na função custo. Logo,

3) Seja a receita média de vendas para um determinado produto. Determine a receita máxima obtida.

1º) Determinar a função Receita.

2º) Vamos determinar os pontos críticos.

Resolvendo a equação , tem-se , cujas raízes são dadas por: e .

3º) Aplicar o teste da 2ª derivada para determinar qual ponto é de máximo.

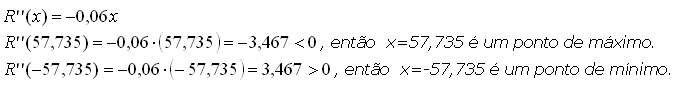
4º) Determinar a receita máxima

Para encontrar o valor da receita máxima é só substituir , que é a abscissa correspondente ao ponto de máximo, na função receita. Logo,