Devemos lembrar que a toda função matemática corresponde um gráfico, como, por exemplo, retas, associadas às funções do primeiro grau, e parábolas, associadas às funções do segundo grau (isto para não falar nas funções exponenciais, logarítmicas e trigonométricas). Assim, esta curva normal também é fruto de uma função que pode ser expressa como:

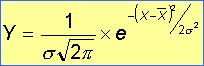
Onde:

O aspecto gráfico, desta distribuição, de forma genérica, é o seguinte:

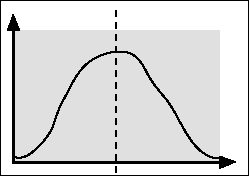
sendo que, no eixo horizontal, são representados os valores da variável que se está estudando e, no eixo vertical, valores associados às frequências relativas correspondentes aos valores específicos da variável sob análise.

A formulação apresentada, com certeza, apresenta uma forma bastante assustadora. Entretanto, felizmente não teremos necessidade de utilizá-la tal como se apresenta. O que a fórmula demonstra é que qualquer distribuição normal é determinada por dois parâmetros: a média e o desvio-padrão dos dados.

Jack Levin, em seu livro Estatística Aplicada a Ciências Humanas, considera a distribuição normal como " um modelo teórico ou ideal que resulta muito mais de uma equação matemática do que de um real delineamento de pesquisa com posterior coleta de dados. Entretanto, a utilidade da curva normal para o pesquisador pode ser evidenciada por meio de suas aplicações a efetivas situações de pesquisa". Escreve, ainda, Jack Levin: "a curva normal pode ser usada na descrição de distribuições de escores, na interpretação do desvio padrão e em afirmações relacionadas com a noção de probabilidade" e "a curva normal constitui um ingrediente essencial para a tomada de decisões estatísticas, a partir da qual o pesquisador pode generalizar para populações as conclusões a que tenha chegado ao lidar com amostras."