Linha de Mercado de Títulos ou Securities Market Line – SML - sabe-se que o Beta é a medida apropriada para o cálculo do risco de um ativo. Entretanto, se o Beta é a medida apropriada para o cálculo do risco de um ativo, qual a relação existente entre o risco de mercado e o retorno esperado? A partir da linha de mercado de títulos ou Securities Market Line – SML é possível construir uma relação que relacione o Beta ao retorno esperado pelo ativo.

De fato, a relação Beta-retorno esperado, formalizada na linha de mercado de capitais ou capital market line – CML, pode ser vista como uma relação entre risco e remuneração. O Beta de um ativo é a medida apropriada de seu risco porque mede a contribuição do ativo sobre a variância da carteira de mercado. Portanto, para qualquer ativo, o prêmio de risco é diretamente proporcional ao próprio Beta. Essa reta, denominada capital market line, descreve todas as carteiras eficientes e relaciona o retorno de uma carteira eficiente a preço do dinheiro no tempo (R_F ) acrescido do prêmio de risco. O prêmio de risco, por sua vez, pode ser decomposto em 2 componentes:

(a) uma medida de risco de um ativo (E(RP) - RF), e
(b) o prêmio de risco do mercado (β_i)

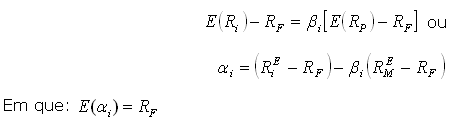
Essa relação entre o retorno esperado e o Beta pode ser representada graficamente como a Linha de Mercado de Títulos. É importante que seja comparada a Linha do Mercado de Títulos ou securities market line – SML com a Linha do Mercado de Capitais ou capital market line – CML.

A CML plota o prêmio de risco de carteiras eficientes (combinações lineares de ativos livres de risco e a carteira de mercado) como função do desvio-padrão da carteira.

A SML, por sua vez, plota o prêmio de risco de ativos individuais (e não apenas carteiras eficientes) como uma função do risco do próprio ativo. Note que a medida relevante de risco para um ativo individual mantido em carteira não é o desvio-padrão ou a variância, mas sim a contribuição dos ativos para a variância da carteira. Por definição, a contribuição dos ativos para a variância da carteira é o próprio Beta.

Ressalte-se, ainda, que, dado certo risco associado a um investimento, expresso pelo seu Beta, a SML provê uma taxa de retorno requerida para compensar o investidor pelo risco. A SML, portanto, provê um benchmark para a análise da performance de certo investimento. De fato, se um ativo está abaixo de seu preço esperado, o retorno esperado em excesso estará acima da SML. Nesse contexto, surge uma oportunidade de arbitragem, que é uma propriedade que se apresenta para o investidor quando existem ativos homogêneos com preços diferenciados em diferentes e próximos mercados onde o custo de transportes é desprezível.