Por analogia, podemos inferir que, caso a fórmula, seja aplicada em uma série antecipada, os fluxos também serão trazidos para um período anterior ao primeiro fluxo da série que, no caso, será o período “-1”, tendo em vista que a série, por ser antecipada, começa no momento “0”.

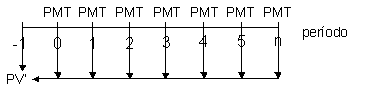
Como desejamos encontrar o valor presente da série hoje (momento 0), após aplicar a fórmula de valor presente para séries postecipadas, devemos capitalizar o resultado por um período, fazendo com que o valor encontrado no período “-1” (PV’) seja levado até o período “0” onde encontraremos PV, assim:

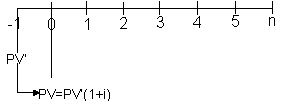
Sendo o valor presente, para séries antecipadas, igual ao do valor presente calculado pela equação que serve para séries postecipadas PV’ capitalizado por um período:

(2)

Sabendo-se que a equação do valor presente de uma série postecipada é:

(3)

Substituindo a equação (3) na (2) teremos:

(4)

A equação (4), que serve para o cálculo do valor presente (PV) de séries uniformes antecipadas, nos diz que este valor pode ser obtido mediante a multiplicação dos termos da série (PMT) pelo fator de valor presente (FPV(i,n)) para uma taxa “i” e um número de termos “n”, capitalizados por um período, ou seja, multiplicados por (1+i).

Exercícios Resolvidos