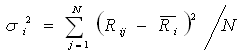2 - Uma medida de dispersão

Não apenas é necessário ter uma medida do retorno esperado, mas também é útil ter uma medida de quanto os resultados diferem da média. Intuitivamente, uma medida sensata seria examinar a diferença diretamente, ou seja, calcular . Tendo determinado a medida de dispersão, para cada resultado bastaria totalizar essas medidas.

Entretanto, essa abordagem apresenta um problema. Algumas diferenças serão positivas, enquanto outras serão negativas e tenderão a se anular. Há duas alternativas para resolver este problema:

• tomar valores absolutos das diferenças, ou
• elevar ao quadrado as diferenças. Ressalte-se, contudo, que ao analisarmos as carteiras, ao invés de um único ativo, a segunda solução é mais adequada.

De fato, o cálculo do quadrado das diferenças observadas em relação à média é a representação da variância. Em termos formais, a variância do retorno do ativo i, denotado por , é dada por:

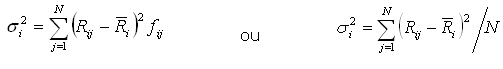
As fórmulas acima representam a variância populacional, contudo, freqüentemente, o cálculo da variância é obtido com base em valores históricos. Nesse caso, o estimador da variância não viesado é dado por: