A variância da combinação de ativos - Essa simples análise nos fornece os elementos mediante os quais um investidor pode escolher entre ativos de risco. Contudo, as opções disponíveis para o investidor não estão restritas a investimentos em um único ativo. Um investidor pode alocar seus recursos em diversos ativos. Enquanto essa oportunidade eleva o número de opções para o investidor, ao mesmo tempo alavanca o grau de complexidade de risco.

O risco de uma carteira é bem distinto da média do risco dos ativos individuais. De fato, para melhor avaliar o risco de uma carteira é necessário considerar a expressão da variância da soma:

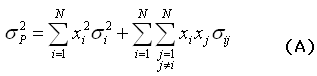
Em que x_i é a participação do ativo i na carteira e a covariância entre os ativos i e j.
Em vários aspectos, é útil explicitar a covariância como um produto dos desvios-padrão dos dois ativos e o coeficiente de correlação de Pearson (P_ij), ou seja,

Desse modo, é possível reescrever (A) como:

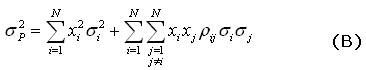
Retornando para (A), o primeiro term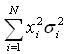o, , expressa a soma das variâncias dos ativos individuais multiplicados pelo quadrado das proporções investidas em cada ativo. O segundo termo é a covariância dos ativos. Observe que cada covariância entre pares de ativos está presente na expressão.

A expressão anterior nos permite inferir algumas estratégias para o investidor. Considere a estratégia de realizar investimentos em iguais proporções. Nesse caso, (A) pode ser reescrita como:

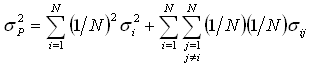
Rearranjando a expressão, obtemos:

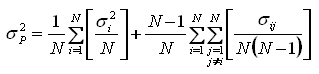
Note que ambos os termos entre colchetes são médias. O primeiro termo é a média das variâncias individuais, enquanto o segundo é a média das covariâncias. Substituindo os somatórios pela expressão das médias:

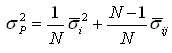
A contribuição da variância individual tende a zero conforme N tende ao infinito.

Contudo, a contribuição da covariância se aproxima da covariância média. Portanto, o risco individual de um ativo pode ser diversificado, mas a contribuição do risco total causada pela covariância não pode ser diversificada.