Para medir o impacto da mudança no risco da carteira, calcula-se a variância da nova carteira, cuja variância ajustada é:

Observe que se δ = 0, então, a variação incremental é dada por:

Dividindo-se a equação (E) pela (F), obtém-se:

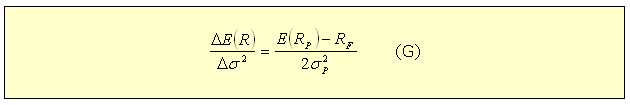
Suponha, agora, que o investidor, ao invés de investir marginalmente na carteira de mercado, invista marginalmente no ativo i financiado por um empréstimo à taxa livre de risco. A nova carteira, composta pela carteira do mercado, tem o ativo i (na proporção δ ) e o ativo livre de risco (na proporção -δ). Então o acréscimo médio do excesso de retorno é:

E o acréscimo de sua variância é dado por:

Desprezando o termo δ² (pois δ = 0) e dividindo a equação (H) pela equação (I):

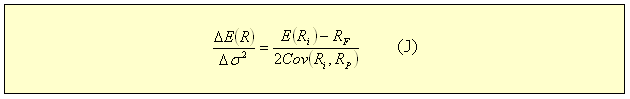
Em equilíbrio, o excesso de retorno do ativo i deve igualar o excesso de retorno do mercado. Em caso contrário, os investidores podem alterar a participação na carteira para incorporar o ativo que produza um excesso de retorno ajustado pelo risco. Essa pressão sobre os ativos fora do equilíbrio conduz a alteração de seus respectivos preços e, conseqüentemente, sobre a taxa de retorno. O processo continua até que o excesso de retorno marginal se iguale ao do mercado.
Nesse contexto, igualando as equações (G) e (J)

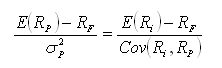
Rearranjando a expressão acima, obtemos:

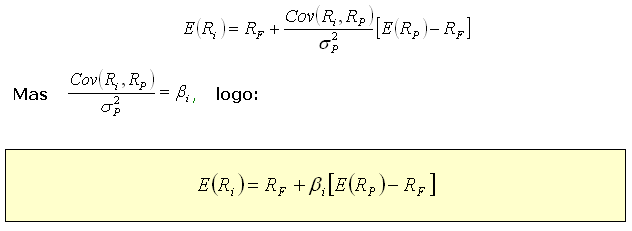
Essa relação entre retorno esperado e o Beta é a formalização da linha de mercado de capitais, ou capital market line – CML e consiste, também, na mais familiar expressão entre os praticantes do CAPM.