3 - Medindo o risco de um ativo Individual em relação ao mercado: a covariância e o Beta


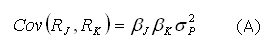
O CAPM baseia-se na hipótese que cada ativo se correlaciona com um único fator: o mercado. Nesse contexto, é possível escrever a covariância entre dois ativos quaisquer como:


Note que a covariância pode ser expressa como o produto de três termos. O último é a variância (δ2P) da taxa de retorno da carteira de mercado. Esse termo evidencia a magnitude dos deslocamentos do mercado. Os outros dois termos ( BJ e BK) mostram a extensão por onde esses ativos respondem a variações do mercado.

É possível reescrever a equação (A) como:

Por definição, β = 1. Logo,

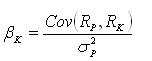
Assim, dada uma carteira C, composta por M ativos, é possível mostrar que:

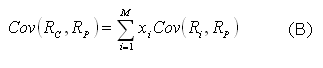
Dividindo-se ambos os lados da equação (B) por δ2p , obtém-se o Beta ( βC ):

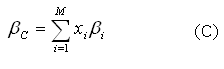
O Beta ( βC ) é uma medida de correlação entre um ativo financeiro ou um portfolio e o mercado como um todo; é o nome dado ao coeficiente que mede a sensibilidade das taxas de retorno de um portfolio ou de um ativo financeiro, em relação aos movimentos do mercado; é chamado de índice de risco sistemático, ou seja, o risco sistemático do título expresso em unidades do risco de mercado.

Para qualquer carteira, o Beta ( βC ) da carteira será uma média ponderada dos Betas dos ativos individuais que a compõem.

Outra importante conclusão que pode ser extraída da equação (B) diz respeito à contribuição da variância de um ativo individual para a variância do mercado. De fato, a equação (B) é válida para qualquer carteira, inclusive a carteira de mercado (P).

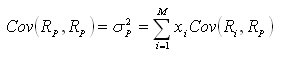
A equação acima mostra que a contribuição de um ativo individual para a variância da carteira de mercado é medida pela covariância do ativo e o mercado. Ressalte-se, ainda, que o fator Beta é igual à razão da covariância entre o ativo e o mercado pela variância do mercado.

Portanto, é sempre possível medir o risco de um ativo de dois modos alternativos:

a. por sua covariância com o mercado, ou
b. pelo Beta. Em função de seu apelo intuitivo e simplicidade, o Beta surge como uma medida mais utilizada.


Copyright © 2006 AIEC.