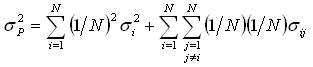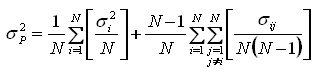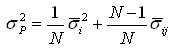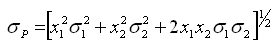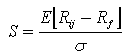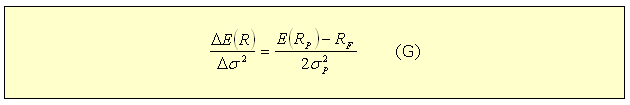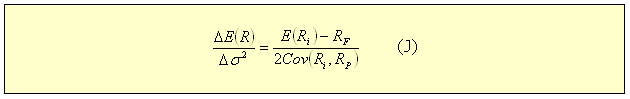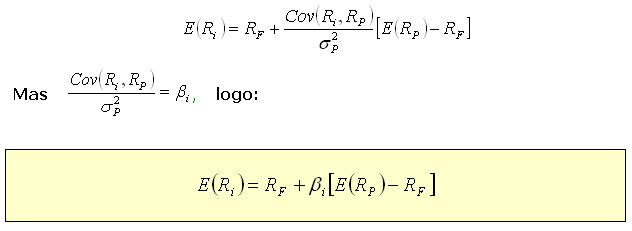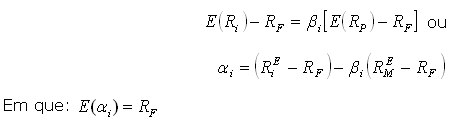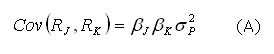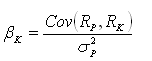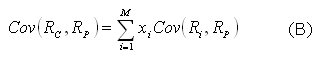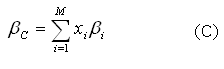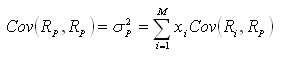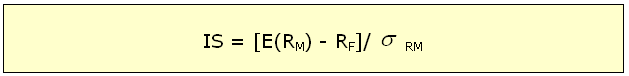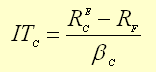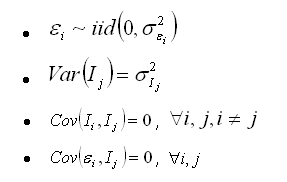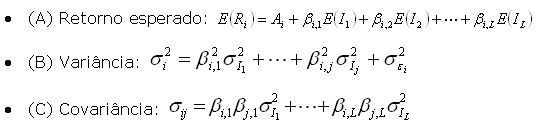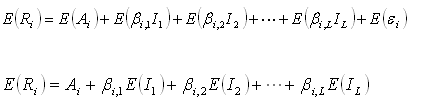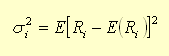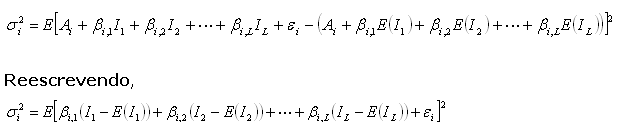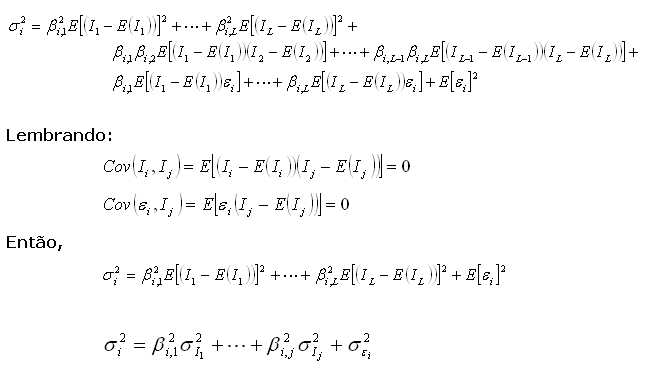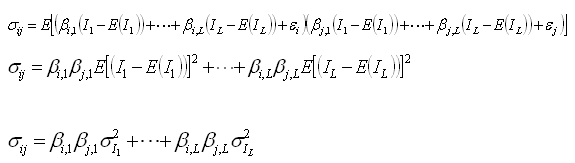Nesse cenário,
um investidor, quando defrontado com um instrumento financeiro, cuja remuneração
dependa da realização de um determinado estado da
natureza, deve calcular uma expectativa de retorno para cada
risco. O retorno esperado, denotado por ![]() ,
é dado por:
,
é dado por:
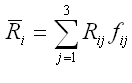
Em que Rij � o retorno do ativo i no estado da natureza j e fij é a probabilidade associada à ocorrência do retorno do ativo i no estado da natureza j. No caso em tela, o retorno esperado para o ativo i é igual a 9.
Quando o investidor opta por diversificar seus investimentos entre diversos instrumentos financeiros, o cálculo da expectativa de retorno de uma carteira deve considerar o retorno esperado de cada ativo, assim como a composição dos ativos em carteira. A título de ilustração, considere os dados da tabela seguinte:
| Estado
da Natureza |
Probabilidade |
Ativo
1 |
Ativo
2 |
Ativo
3 |
|
1 |
1/3 |
6 |
12 |
42 |
|
2 |
1/3 |
10 |
20 |
30 |
|
3 |
1/3 |
14 |
28 |
18 |
|
Retorno
Esperado |
10 |
20 |
30 |
|
Supondo que o investidor tenha combinado os ativos 1, 2 e 3 nas proporções de 30%, 30% e 40%. Nesse caso, a remuneração esperada pelo investidor é de 21% [=(0,3x10)+(0,3x20)+(0,4x30)].
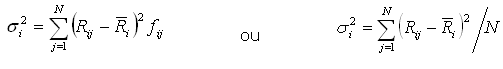
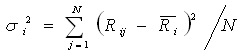
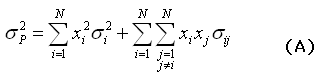
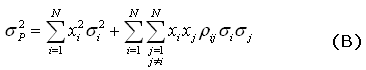
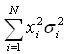 ,
expressa a soma das variâncias dos ativos individuais multiplicados
pelo quadrado das proporções investidas em cada ativo. O
segundo termo é a covariância dos ativos. Observe que cada
covariância entre pares de ativos está presente na expressão.
,
expressa a soma das variâncias dos ativos individuais multiplicados
pelo quadrado das proporções investidas em cada ativo. O
segundo termo é a covariância dos ativos. Observe que cada
covariância entre pares de ativos está presente na expressão.