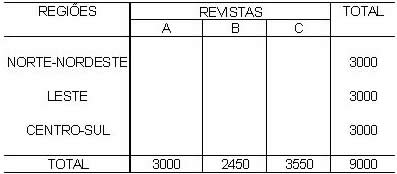
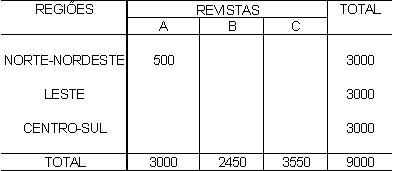
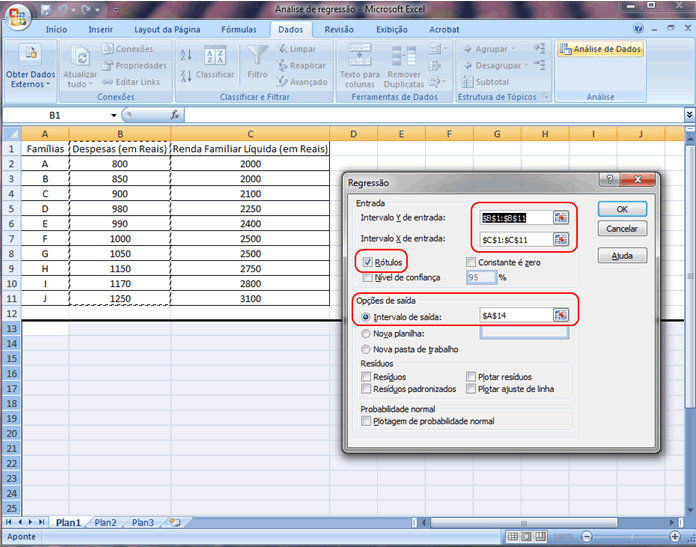
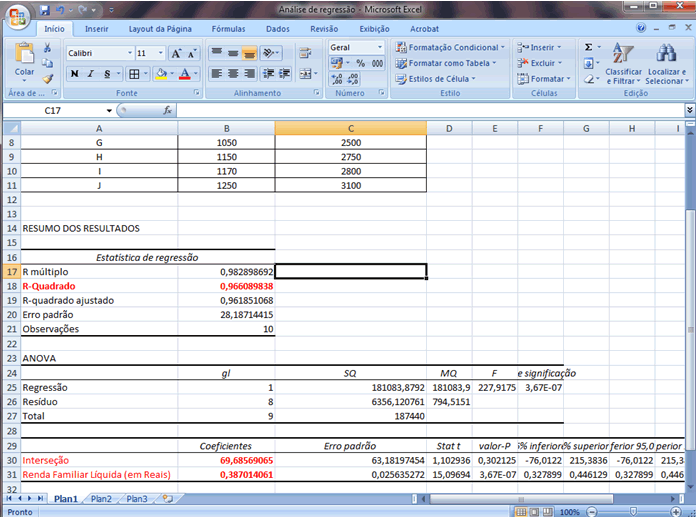
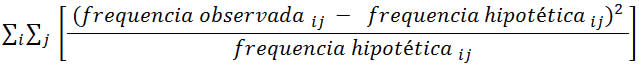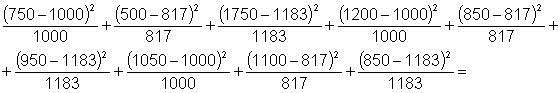1 - Caracterização da Análise Bidimensional

Nos estudos anteriores nossa análise recaiu sobre o comportamento de uma variável estudada de forma "individual", ou seja, não relacionada com outra(s).

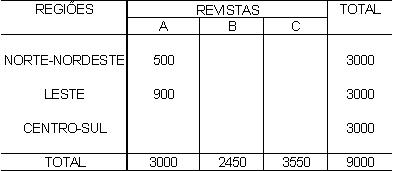
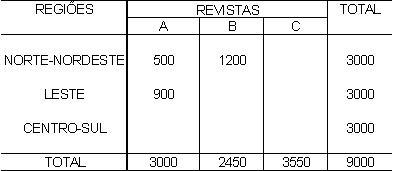
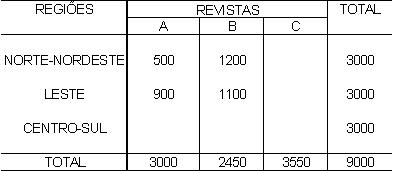
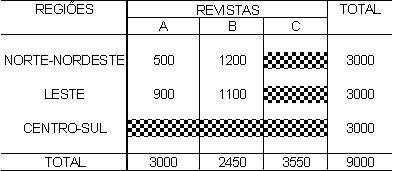
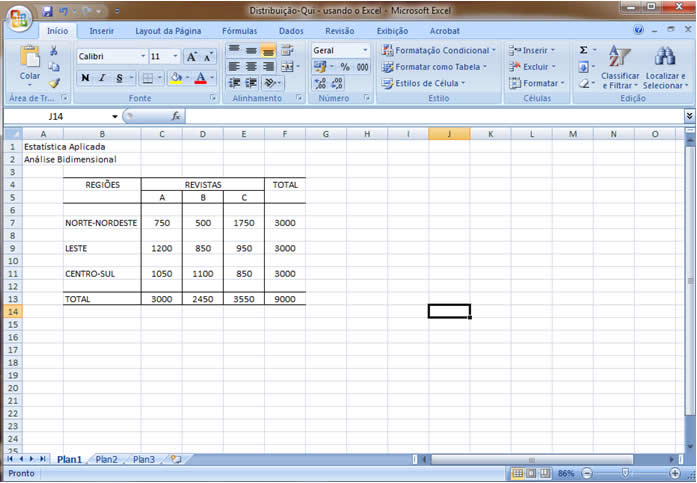
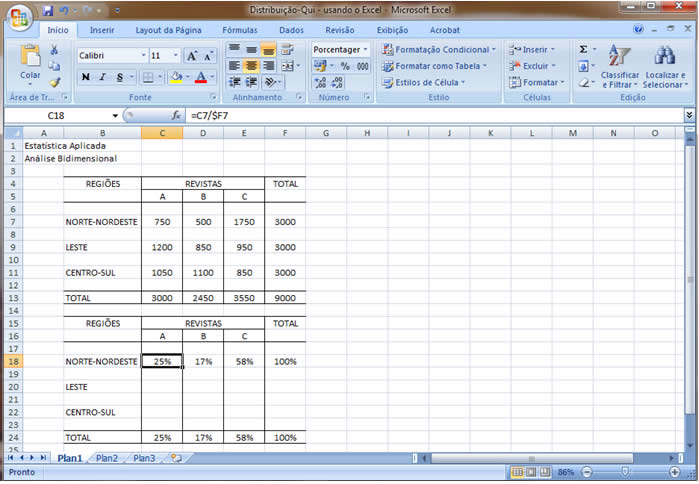
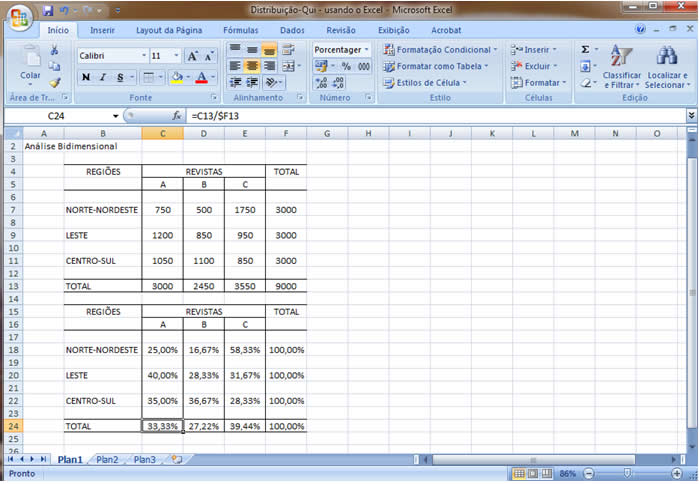
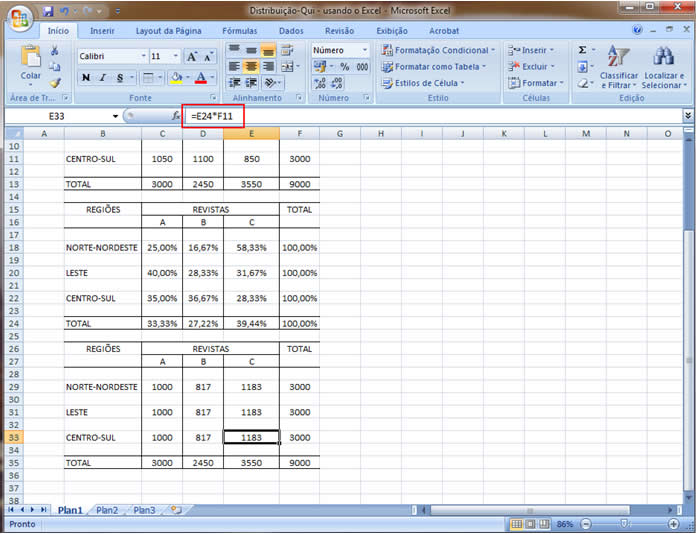
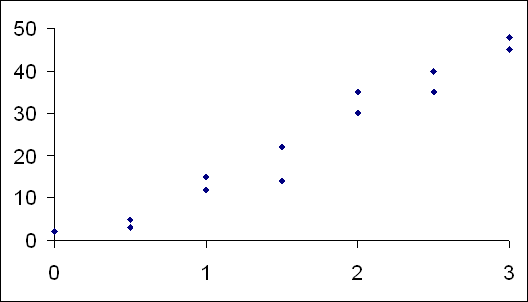
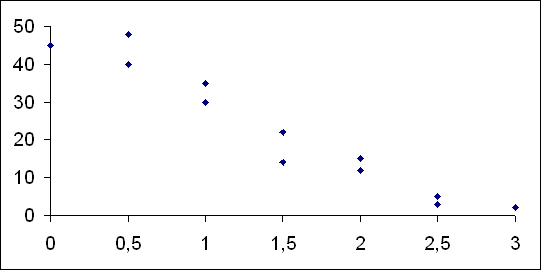
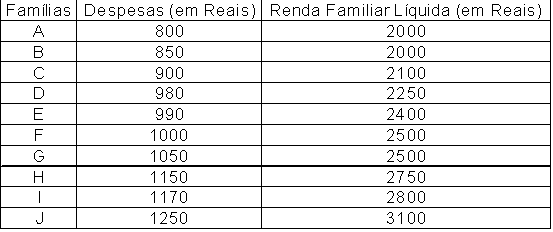
A partir de agora nossa atenção estará voltada para análise de duas variáveis observadas simultaneamente em um conjunto de indivíduos/objetos, de forma que os diferentes "níveis" das duas variáveis aparecerão cruzados/inter-relacionados, mostrando, efetivamente, um comportamento conjunto.

Existem dificuldades práticas para geração das medidas descritivas quando a variável não é tipicamente quantitativa. Essa técnica de análise permite que variáveis quantitativas e qualitativas (tanto ordinais como nominais) possam ser tratadas, em três diferentes combinações, como:

O exemplo abaixo nos mostra a relevância desta abordagem.

Um anunciante com uma grande verba para investir em publicidade suspeita que a preferência dos leitores por revistas semanais de circulação nacional independe das regiões geográficas onde moram. Considerando que uma nova revista semanal entrou em circulação, imagine que, após algumas semanas de vendas, fez-se uma pesquisa com 9000 leitores de três regiões do país (3000 em cada uma delas).

Cada um daqueles leitores, depois de ler as edições de um mês de cada revista, deveria escolher uma delas, manifestando sua preferência. Os resultados foram:

Se você for contratado para dar seu parecer para este anunciante, o que você concluiria em seu relatório? A premissa do anunciante está correta? Por quê?

Essa é uma situação que envolve a análise de duas variáveis simultaneamente (o comportamento conjunto de duas variáveis, sendo que ambas são qualitativas nominais: região geográfica e preferência por uma revista). Aqui podemos estabelecer duas hipóteses que devem ser avaliadas:

O primeiro passo é ter uma ideia dos percentuais associados à realidade apresentada, uma vez que as frequências absolutas, tais como foram lançadas, podem induzir uma visão equivocada do que de fato está acontecendo.

É importante estabelecer com clareza que, caso haja relacionamento/associação entre as variáveis em questão, a preferência estaria sendo impactada pela região de residência do leitor e não o contrário.

Também é muito importante deixar suficientemente claro que em nenhum momento está sendo insinuado que uma das hipóteses está vinculada à não existência de uma preferência bem caracterizada por alguma das revistas.

O que isso quer dizer? Quer dizer que não estamos querendo saber qual a revista seria mais lida, ou seria a melhor escolha. O que estamos querendo saber é se a escolha da revista está ou não relacionada com a região do leitor.

Assim, o que está em questão é se o perfil de preferência nas três regiões geográficas pode ser considerado aproximadamente o mesmo (o que caracteriza um quadro de não relacionamento, contemplado pela hipótese H0) ou se há padrões de preferência distintos para as regiões investigadas.

Feitas essas considerações, a tabela com as frequências percentuais ficaria:

Clique aqui e veja como cada um dos percentuais acima foi obtido.

Essa tabela parece revelar algum grau de dependência/relacionamento entre as variáveis região de residência do leitor e preferência por revista semanal de circulação nacional, uma vez que, se não houvesse, seriam esperadas proporções próximas a 33,33%; 27,22% e 39,44% em cada uma das regiões (de tal modo que não seria possível a identificação da região, caso fosse dado o perfil de preferência, ou, em outras palavras, para todas as regiões valeria o padrão de preferência revelado para o Brasil como um todo).

Dito de outra forma, se a distribuição de preferência considerando todas as regiões é 33,33%; 27,22% e 39,44%, então caso a preferência fosse independente da região, encontraríamos essa mesma proporção em todas as regiões. Por exemplo, para a revista A na região Norte-Nordeste, teríamos 33,33% do total da região, ou seja, 33,33% * 3000 = 1000. Para a revista B teríamos 27,22% do total, nesse caso 27,22%*3000 = 817 e, por fim, para a revista C teríamos 39,44% * 3000 = 1183.

Assim, as respectivas frequências hipotéticas para essa situação (de independência) seriam:

Clique aqui e veja como cada uma das frequências desse quadro foi obtida.

Outra observação que se torna necessária, por ser oportuna e muito importante, é que o fato de haver frequências idênticas nas três regiões (nesse caso, 3000 leitores) foi meramente ilustrativo e com efeito didático. Na prática, isso pode ocorrer ou não, e o procedimento até agora adotado fica inalterado.

Na situação que está sendo discutida, fica nítido que há "desvios" entre as frequências observadas (reais) e as frequências esperadas (hipotéticas, no caso da independência ser verdadeira). Devemos ser capazes de responder se estas diferenças são suficientemente grandes ou pequenas (a resposta a essa pergunta vai efetivamente validar uma das duas hipóteses levantadas).

É necessário, então, definir um critério objetivo que nos auxilie nessa tarefa. Por analogia com a lógica utilizada para a definição de variância, podemos chegar à seguinte medida:

O que está sendo indicado é que se deve tomar cada frequência de fato observada e subtrair a correspondente frequência hipotética. Em seguida, deve-se elevar esse resultado ao quadrado para que não se tenham valores negativos, como no cálculo de variância, e então dividir pela frequência hipotética para que se tenha uma ideia mais adequada da diferença entre as frequências.

O raciocínio poderia ser também assim.

Passemos agora ao cálculo desse "indicador":

Cujo resultado final fica:

É indispensável, agora, concluir se o valor de 738,75 (unidades de medida) reflete uma grande diferença entre a situação real e a hipotética ou, se na verdade, a diferença não pode ser considerada significativa. Para que essa decisão seja possível, será necessário abordar dois novos aspectos teóricos:

Estudaremos esses conceitos a seguir.

2 - Graus de Liberdade

Para termos uma noção intuitiva do que vem a ser o número de graus de liberdade, é indicado realizar a análise de uma tabela de dupla entrada.

Considere que seja apresentada uma tabela contendo apenas os totais parciais, como mostrado a seguir:

Os totais parciais espelham com fidelidade o resultado da pesquisa realizada quando analisada cada variável separadamente. O que está em questão é o comportamento conjunto das duas variáveis.

Considere agora que podemos arbitrar um valor para preenchimento do cruzamento: revista A e região Norte-Nordeste. Qualquer número entre 0 e 3000 pode ser escolhido, uma vez que não estará ultrapassando os limites impostos pelos totais parciais (tanto total da linha como da coluna).

Admita que seja escolhido o número 500 (como poderia ter sido 600, 700 ou outra opção):

Façamos agora o mesmo para o cruzamento da revista A com região geográfica Leste. Embora já não tenhamos tantas opções de números, pois a primeira célula já foi preenchida, continuamos com um bom leque de alternativas. Admita, mais uma vez, por hipótese, que seja escolhido o número 900:

O que você acha que acontece agora para o preenchimento do cruzamento revista A e região Centro-Sul? Existe alguma liberdade de escolha do número que irá ocupar aquela célula?

Caso queiramos preservar os totais da primeira coluna e da terceira linha não há alternativa que não seja o número 1600. Assim, podemos dizer que, ao preencher "com liberdade" as duas primeiras células, a terceira ficou "presa", "automaticamente" condicionada a elas.

Esse raciocínio pode continuar sendo desenvolvido agora para o cruzamento: revista B e região Norte-Nordeste. Mais uma vez, embora não haja tantas opções disponíveis (se compararmos com as possibilidades da primeira célula, na qual inserimos o 500), há um número considerável de alternativas, e podemos, por exemplo, optar por 1200. A tabela ficaria:

Se pensarmos no preenchimento do cruzamento revista C e região Norte-Nordeste, é fácil constatar que só há uma possibilidade que atende corretamente à condição de 3000 leitores naquela região, a saber, o número 1300.

Mais uma vez, não há "liberdade" de preenchimento para aquela célula. Para o cruzamento revista B e região Leste, por analogia com as demais situações, há diversas possibilidades numéricas que podem ser consideradas.

Pode-se arbitrar, por exemplo, 1100 e assim a tabela estaria completa, pois tanto o cruzamento revista B e região Centro-Sul, como o cruzamento revista C e região Centro-Sul ficariam "atrelados":

A constatação que se quis passar é que em uma tabela com três linhas e três colunas, uma vez fixados/arbitrados quatro valores, os outros cinco ficam a eles condicionados, e fica visível que a "perda de liberdade" se dá em uma linha e uma coluna:

As células hachuradas significam apenas que estão "presas", condicionadas ao preenchimento das demais. Logo, pelo exposto:

Número de graus de liberdade = (número de linhas - 1) X (número de colunas - 1)

No caso em questão, como há 3 linhas e 3 colunas: (3 - 1) x (3 - 1) = 2 x 2 = 4

Como visto no cálculo da medida de diferença entre as situações real e hipotética, havia a soma de nove parcelas, fruto da existência de três linhas e três colunas. O número de graus de liberdade está vinculado ao tamanho da tabela, ou seja, ao número de linhas e colunas, uma vez que parece razoável supor que à medida que o número de células aumenta, a medida da diferença entre as duas situações (real e hipotética) tende a aumentar. Isso significa que o resultado da diferença para uma determinada tabela pode ter interpretação distinta do mesmo resultado para outra tabela maior ou menor.

Resumo

Na análise bidimensional, é estudado o comportamento conjunto de duas variáveis, que tanto podem ser quantitativas como qualitativas. O objetivo maior é concluir se há independência ou dependência entre elas (relacionamento ou não).

Dada uma situação para a qual foram observadas frequências relativas ao cruzamento das diferentes respostas de uma variável com as diferentes respostas de outra, parte-se para a determinação de frequências percentuais, com o cuidado de verificar qual variável influencia o comportamento da outra, caso exista relacionamento entre elas.

Feito isto, parte-se para a determinação de um conjunto de frequências hipotéticas, admitindo-se que a independência fosse verdadeira. Isso permitirá uma comparação com as frequências verdadeiras, a partir do cálculo de uma medida da diferença entre os conjuntos de frequências. Essa medida, denominada qui-quadrado servirá para analisarmos se existe um relacionamento entre as duas variáveis e será desenvolvida no próximo módulo.

Vimos ainda que só poderemos interpretar corretamente o resultado obtido conhecendo o número de graus de liberdade.

O número de graus de liberdade está vinculado ao tamanho da tabela, isto é, ao número de linhas e colunas, uma vez que parece razoável supor que à medida que o número de células aumenta, a medida da diferença entre as duas situações (real e hipotética) tende a aumentar. Isso significa que o resultado da diferença para uma determinada tabela pode ter interpretação distinta do mesmo resultado para outra tabela maior ou menor.

1 - Distribuição Qui-Quadrado

Para compreendermos o conceito da distribuição qui-quadrado, será feita a analogia com a distribuição de renda brasileira, que é assimétrica e assemelhasse bastante ao seguinte aspecto:

O que está sinalizado é que à medida que a renda aumenta, a quantidade de pessoas que ganha aquela quantia vai diminuindo sensivelmente. Esse aspecto é típico de uma distribuição denominada qui-quadrado (muito embora o gráfico desse tipo de distribuição possa ser bastante distinto, dependendo do número de graus de liberdade). O símbolo adotado para essa distribuição é:

A decisão, se uma determinada renda é considerada grande ou pequena, passa por uma avaliação comparativa, afinal um mesmo salário pode ser considerado baixo em um contexto e alto em outro. Assim, ao indagar se um salário de 50 unidades monetárias, por exemplo, é alto ou baixo, deve-se ter uma ideia da frequência percentual que fica abaixo e acima desse valor.

Caso tenha-se uma proporção de 95 ou 99% abaixo do valor de referência (e, consequentemente, 5 ou 1% acima, respectivamente), teremos de admitir que aquele valor pode ser considerado alto. O procedimento para a avaliação no nosso contexto é análogo: se formos capazes de determinar qual o percentual que fica acima e qual fica abaixo do valor calculado, teremos um indicador nítido de sua ordem de grandeza.

É com base nesse conceito que iremos aplicar a distribuição qui-quadrado na análise bidimensional, pois vimos no módulo anterior que chegamos a calcular um valor que representava a diferença entre a frequência real e a hipotética, lembra-se? Pois bem, o problema é que não sabíamos se o valor obtido era grande ou pequeno. Se a diferença fosse grande, então a hipótese que dizia que a preferência variava com a região seria confirmada. Caso o valor fosse pequeno, ou seja, a diferença entre as frequências reais e as hipotéticas fosse pequena, então poderíamos concluir que a preferência não variava com a região do leitor.

Pode-se, então, optar entre duas alternativas para determinação se o valor calculado para a diferença entre a tabela real e a hipotética é suficientemente grande ou não:

(a) recorrer à tabela qui-quadrado, disponível na grande maioria dos livros de Estatística Básica (Mario Triola; Wilton Bussab; Pedro Morettin). O primeiro passo é determinar o número de graus de liberdade para, em seguida, consultar na linha correspondente a esse número um conjunto de probabilidades que irão sinalizar como posicionar/avaliar o valor calculado;

Exibimos, a seguir, um trecho da tabela A-4 que se encontra no livro de Mario Triola, (1999) pág. 356:

Constata-se que, para 4 graus de liberdade, o valor 14,860 "quebra" a distribuição qui-quadrado deixando 99,5% dos valores à sua esquerda e 0,5% à sua direita.

Consequentemente, o próprio 14,86 já poderia ser considerado um valor suficientemente grande para esse caso. O que dizer então do valor resultante de nossa medida, ou seja, 738,75? Parece inquestionável que esse valor seja de fato muito grande. Logo, como a diferença "medida" entre as duas tabelas (real e hipotética) é muito grande, e a situação hipotética parte do pressuposto de independência das variáveis, nossa conclusão é:

(b) recorrer à planilha Excel, com essa sequência de comandos, após posicionar o cursor na célula na qual se deseja a inserção do resultado: fx, Estatística, DIST.QUI, OK, e então teremos a seguinte janela.

Deve-se agora digitar o valor calculado de 738,75 ao lado do X e digitar 4 no campo destinado aos graus de liberdade, em seguida OK (observe que antes de clicar em OK já é possível visualizar o resultado).

O resultado mostrado pela planilha revela que a frequência relativa à esquerda do valor 738,75 é muitíssimo baixa, tanto é que foi usada a notação exponencial.

Você consegue imaginar quão pequeno é esse número? Logo só há uma conclusão possível:

O valor calculado para a diferença entre a situação real e a hipotética recebe o nome de qui-quadrado calculado.

Dizer que existe relacionamento entre as variáveis estudadas, embora já agregue significativo valor à nossa análise, ainda deixa margem a uma pergunta muito interessante: que associações foram mais relevantes (mais contribuíram) para a rejeição da independência?

Para responder devem ser consideradas as maiores parcelas da soma que gerou o qui-quadrado calculado (expressam as maiores diferenças entre a situação hipotética de independência e a situação real), até o limite dado pelo número de graus de liberdade. No exemplo dado, são quatro graus de liberdade, então devem ser analisadas as quatro maiores parcelas da soma. Isso não deve ser visto de forma cartesiana, mas sim como uma regra que deve orientar a análise/interpretação da situação, pois a 5ª maior parcela pode ser muito próxima da 4ª maior, merecendo, então, ser incluída no rol das análises mais pontuais. Por outro lado, apenas as três maiores poderiam "esgotar" praticamente a totalização do qui-quadrado calculado, não sendo necessário fazer uma análise específica de mais uma parcela.
Voltando à expressão que gerou o 738,75:

Partindo para as interpretações específicas, as quatro maiores parcelas são, pela ordem:

1. Número de leitores da região Norte-Nordeste que prefere a revista C é significativamente maior do que aquele que seria esperado em uma situação de independência, ou seja, caso o padrão nacional de preferência valesse para todas as regiões indistintamente. Saiba +
2. Número de leitores da região Norte-Nordeste que prefere a revista B é significativamente menor do que aquele que seria esperado em uma situação de independência.
3. Número de leitores da região Centro-Sul que prefere a revista B é significativamente maior do que aquele que seria esperado em uma situação de independência.
4. Número de leitores da região Centro-Sul que prefere a revista C é significativamente menor do que aquele que seria esperado em uma situação de independência.

2 - "Medindo" a Dependência

Uma vez rejeitada a independência, isto é, existe associação entre as variáveis, já se tem um "sentimento" a respeito do grau de associação a partir do valor do qui-quadrado calculado (ou seja, quanto maior for o valor calculado para o qui-quadrado, maior o grau de associação existente). Isso, no entanto, pode soar um tanto subjetivo e de difícil dimensionamento do que venha a ser uma alta ou baixa associação. Assim, Pearson desenvolveu o coeficiente de contingência C, definido por

Onde n é o número de observações.

Do ponto de vista teórico, esse coeficiente é um número entre zero e um. Fica claro que o valor zero ocorre quando se tem um caso de independência "total" (ou "perfeita"). Uma variação possível para C é

Onde t = mínimo entre o número de colunas e o número de linhas da tabela.

Do ponto de vista prático, o percentual à direita do valor do qui-quadrado calculado acaba sendo um "termômetro" muito mais calibrado a respeito da intensidade da dependência presente entre as variáveis.

3 - Utilizando o Excel

Mais uma vez a planilha Excel pode ser um recurso valioso para a prática da análise bidimensional, permitindo, particularmente, um ganho expressivo de tempo, principalmente quando as tabelas são de porte maior do que a apresentada anteriormente.

Uma vez aberta uma planilha, deve-se entrar com os dados em um formato similar ao apresentado a seguir:

Note que, para a linha e a coluna destinadas à inserção dos totais, deve-se introduzir as fórmulas adequadas para que o cálculo das somas seja executado.

Em seguida, prepara-se uma tabela com as frequências percentuais (lembrando a necessidade de considerar qual variável seria condicionada pela outra, caso houvesse relacionamento das variáveis estudadas).

Observe atentamente como foi obtido cada percentual das planilhas apresentadas.

O próximo passo é calcular as frequências hipotéticas a partir dos percentuais resultantes nas posições C24, C25 e C26, multiplicando-os pelas frequências totais encontradas nas posições F7, F9 e F11. Assim:

Deve-se agora construir uma tabela na qual apareçam as parcelas que totalizarão o qui-quadrado calculado. Para o cruzamento revista A e região Norte-Nordeste, lembrando que a medida geral é dada por

faz-se: =((C7-C29)^2)/C29. Para os demais cruzamentos o procedimento é o mesmo.

A pequena diferença entre o valor do qui-quadrado calculado com a utilização do Excel e aquele apresentado anteriormente (738,75), deve-se, unicamente, ao fato de que agora não foram feitas aproximações numéricas para realização dos cálculos.

Uma vez determinado o qui-quadrado calculado, a sequência deve ser exatamente aquela já discutida:

1. Utilização do recurso da planilha para obtenção do percentual à direita desse valor.

2. Decisão pela dependência ou independência.

3. Concluindo-se pela dependência, análise dos cruzamentos que mais contribuíram para rejeição da independência.

Resumo

Vimos que a análise bidimensional estuda o comportamento conjunto de duas variáveis, tendo como objetivo concluir se há independência ou dependência entre elas (relacionamento ou não). No módulo 1 apresentamos um problema que consistia em verificar se a hipótese variável A (Quantidade de revistas) varia em função da variável B (região do país). Para responder de forma conclusiva a essa questão, calculamos quais seriam as quantidades vendidas, caso essa hipótese não fosse verdadeira (as chamadas frequências esperadas). Por fim, calculamos um valor que representa a diferença entre as frequências reais e as frequências esperadas. Mas como interpretar esse valor? Como ele pode nos dizer se as duas variáveis são ou não independentes?

Para responder a essas perguntas, estudamos neste módulo a distribuição qui-quadrado. A distribuição qui-quadrado representa o valor da dispersão para duas variáveis. Tomando por base o valor obtido e o número de graus de liberdade, usa-se a tabela da distribuição qui-quadrado ou a planilha Excel. Quanto maior o valor de qui-quadrado, maior será a dependência entre as duas variáveis. De maneira geral, a literatura rejeita a hipótese de independência quando a área à direita do valor seja inferior ou igual a 0,5%. Chamamos esse valor limite também de grau de significância.

Vimos ainda que, caso haja um relacionamento entre as variáveis, podemos investigar quais os cruzamentos que mais contribuíram para que isto acontecesse. Para tanto, tomam-se as maiores parcelas do qui-quadrado calculado (em número igual ao de graus de liberdade), o que constituirá um bom indicativo do comportamento das variáveis em questão. Por fim, vimos que também é possível usar o coeficiente de contingência de Pearson para medir a dependência entre as duas variáveis.

1 - Caracterizando a análise de regressão

Muitas vezes procuramos identificar a existência de uma relação entre duas ou mais variáveis. Às vezes desejamos verificar, por exemplo, se o nível salarial das pessoas está relacionado com o tempo de experiência profissional da mesma. Pode-se ainda querer saber qual seria o valor de um apartamento de seis quartos em determinado local, onde só se tem a venda apartamentos de 3, 4 e 5 quartos. Por outro lado, pode-se ainda querer saber qual será a estimativa de consumo de energia elétrica de um determinado local ao longo do tempo.

Com o auxílio de uma análise de regressão poderemos conhecer esses valores.

Contudo a correlação (verificação da existência e do grau de relação entre as variáveis) entre os dados deve ser verificada. Em função desse índice, que é conhecido como “coeficiente de correlação”, poderemos chegar ao coeficiente de determinação, que servirá então para validar equação de regressão encontrada para os dados.

A equação alcançada pela análise de regressão será do tipo Y = f(Xi), ou seja, a variável Y será a variável dependente ou explicada pela (s) variável (is) Xi, que será (ão) a (s) variável (is) explicativa (s) ou independente (s). Se a variável dependente estiver em função de somente uma variável independente, diz-se que o modelo (equação) encontrado é simples. Caso a variável dependente esteja em função de mais de uma variável independente diz-se que o modelo é composto.

A função para determinação da variável dependente da relação entre as variáveis. As formas mais usuais são as funções: linear, potência, exponencial, hiperbólica, polinomial e logarítmica.

De uma maneira geral, até pela facilidade das operações matemáticas, a função linear é a mais utilizada. A análise simples, com apenas uma variável independente também é a mais utilizada. Dessa maneira, passaremos então, a detalhar as funções de regressão lineares simples.

Uma equação de regressão linear simples pode ser escrita da forma genérica Y = aX + b, onde X será a variável independente; Y será a variável dependente, que será calculada em função do valor de X; “a” e “b” serão os parâmetros da função.

Analisando a “nuvem” de pontos assinalados, teremos melhores condições de especificar a função que relaciona as variáveis. No caso em análise, o ajustamento pelo modelo linear se dará em termos de uma reta. Contudo nos faltará ainda saber por onde passará a nossa reta. Assim teremos então que calcular os valores dos parâmetros “a” e “b”.

A fim de se otimizar a equação de regressão, esses parâmetros deverão ter valores que aproximem, ao máximo, a reta dos pontos assinalados no diagrama de dispersão, conforme demonstrado na figura a seguir:

Dessa forma, o melhor método para a determinação dos parâmetros “a” e “b” que minimize as discrepâncias entre a reta e os pontos dos pares ordenados dos dados é o Método dos Mínimos Quadrados Ordinários. Segundo esse método, poderemos avaliar os parâmetros “a” e “b” pela aplicação das seguintes fórmulas:

, onde e

e ainda:

Para avaliar o grau de relação entre as variáveis, deveremos determinar o coeficiente de correlação entre das variáveis em estudo através da formulação matemática:

onde:

“n” será o tamanho da amostra.

será o somatório dos valores de “X” multiplicados pelos valores de “Y” um a um.

será o somatório de todos os valores da variável “X”.

será o somatório de todos os valores da variável “Y”.

será o somatório de cada um dos valores da variável “X” elevado ao quadrado.

será o somatório de cada um dos valores da variável “Y” elevado ao quadrado.

O valor de “r” poderá variar de -1 a +1 passando, obviamente pelo zero. Assim, sua interpretação dependerá de seu valor numérico e de seu sinal.

Quando o valor de r estiver compreendido entre zero e 1, significa que temos uma correlação positiva, ou seja, para um incremento positivo da variável independente “X” teremos um incremento positivo da variável dependente “Y”.

Assim, a representação no eixo cartesiano seria da seguinte forma:

Quando o valor de r estiver compreendido entre -1 e zero, significa que temos uma correlação negativa, ou seja, para um incremento positivo da variável independente “X” teremos um incremento negativo, ou ainda um decréscimo positivo da variável dependente “Y”.

Assim, a representação no eixo cartesiano seria da seguinte forma:

Por último devemos validar a equação da reta encontrada. Esse procedimento deve ser efetuado através do coeficiente de determinação, que nada mais é, em termos matemáticos, que o quadrado do valor do coeficiente de correlação:

Teoricamente o coeficiente de determinação é o valor da variação da variável dependente Y, que é explicado pela reta de regressão. Para chegarmos a um valor de r² igual a 0,89, poderemos dizer que 89% da variação total da variável dependente Y está sendo explicada pela reta de regressão em função da variável independente X. Por outro lado 11% da variação de Y permanecem não explicados.

Segundo o Assis (2000) em função do valor do coeficiente de determinação, a mesma pode ser:

Passemos, agora, a um exemplo do emprego da análise de regressão, para resolver um questionamento do dia a dia:

Você pretende abrir um negócio, cujo foco recai sobre produtos alimentícios. Dentro de seu planejamento, você começa a prospectar possíveis pontos para a instalação de sua mercearia / minimercado / “sacolão”. Surgindo um, que lhe chame particular atenção, parte-se para o levantamento de dados junto a um conjunto de 10 famílias (que servirão de base amostral) das circunvizinhanças para tentar ter uma visão preliminar dos gastos mensais que realizam com produtos alimentícios naquela região de seu interesse.

Os dados coletados revelam que:

Você poderia fazer uma análise descritiva, iniciando pelo cálculo da despesa média, passando pelo cálculo da variabilidade, verificação da existência de pontos discrepantes, mas você está muito intrigado com possíveis explicações para a variação das despesas entre as diferentes famílias, daquela área da cidade. Surge logo uma potencial explicação: a renda das famílias. Como você montou um cadastro, no qual também constam informações sobre a renda familiar (admitindo que as famílias entrevistadas não fizeram nenhuma restrição para informar esse dado), vem a tabela:

Busca-se então construir uma equação de regressão linear simples relacionando a variável de interesse dependente (despesas mensais com alimentação), designada por Y, e a variável que supostamente irá explicá-la (renda mensal líquida), designada por X. Assim, o que se busca é uma expressão do tipo:

Os procedimentos de cálculo, para determinar essa equação de regressão, são os seguintes:

a) Inicialmente identificamos o valor de n (número de pares de elementos amostrais).
n = 10.

b) Calculamos os valores de:, , , , , X , Y assim:

= 2000+2000+2100+2250+2400+2500+2500+2750+2800+3100 = 24.400

c) Na sequência, devemos calcular os valores dos parâmetros Sxx e Sxy:
= 60.745.000 – [10*(2440)2] = 60.745.000 – 59.536.000 = 1.209.000
= 25.209.500 – (10*2.440*1.014) = 467.900

d) Finalmente, poderemos calcular os valores dos parâmetros “a” e “b” de nossa equação de regressão:

= 467.900 / 1.209.000 = 0,39

b = Y - a X = 1.014 – (0,39*2.440) = 62,4

Logo, nossa equação de regressão será: ,o acento circunflexo sobre a variável dependente “Y” significa a estimação desse valor, ou seja, o par ordenado estabelecido não necessariamente pertencerá ao conjunto de dados originais.

Com a equação de regressão estabelecida, passaremos, então, à sua validação estatística. Essa validação deve ser efetuada através do cálculo do coeficiente de determinação r². Para tanto calcularemos o coeficiente de correlação entre as variáveis “r” e elevaremos o valor de seu resultado ao quadrado. Assim:

O resultado do coeficiente de determinação de 0,966, significa que a equação estabelecida entre a variável independente X (renda familiar líquida) e a variável dependente Y (despesas) explica 96,6% a relação que existe entre as mesmas.

Assim, podemos dizer que a determinação foi muito forte e, consequentemente, a equação estabelecida foi validada e poderá ser utilizada para fins de estimação.

Dessa forma, se quisermos estimar qual seria, por exemplo, a despesa de uma família com renda líquida mensal de R$ 5.000,00, bastaria entrar com o valor de 5.000 na equação:

Portanto, a despesa para uma família que possui uma renda familiar de R$ 5.000,00 (cinco mil reais) será de R$ 2.012,10 (dois mil e doze reais e dez centavos).

Por outro lado, qual seria, de acordo com a equação, a expectativa de despesa de uma família que não tivesse nenhum rendimento?

Bastaria substituir o rendimento nulo, ou seja, zero na equação, assim:

A despesa seria de R$ 62,40 (sessenta e dois reais e quarenta centavos).

Resumo

Na análise de regressão busca-se responder por que determinada variável está variando e como ela está variando.

Como uma primeira abordagem recorre-se a um modelo bastante simples, que é a função do primeiro grau, ou seja, Y = aX + b. A partir daí, é necessário estabelecer um critério para determinação dos parâmetros a e b. Esse método será o de mínimos quadrados, o que significa dizer que os valores obtidos serão aqueles que minimizarão a soma dos quadrados dos erros, entendendo como erros (ou resíduos) as diferenças entre os valores reais / observados de Y e aqueles valores estimados a partir da construção do modelo e substituição dos valores de X.

A reta assim obtida será a melhor reta possível, o que não é sinônimo de ser uma boa reta (ou uma reta suficientemente aderente à realidade). Assim, é necessário avaliar o quanto o modelo explica (ou justifica) a variabilidade original de Y. A medida construída para isto é o coeficiente de determinação, que revelará qual o percentual de explicação da variabilidade de Y deve-se à variabilidade de X (dentro do modelo determinado). O próximo passo é interpretar os valores dos parâmetros a e b, sendo que a será o valor de Y, quando X = 0 (o que não necessariamente tem um significado prático) e b será o impacto sobre a variável Y quando X variar de uma unidade (no mesmo sentido se for um valor positivo e em sentidos contrários, caso seja negativo).

Caso o valor do coeficiente de determinação não seja julgado satisfatório, é conveniente "especular" as possíveis razões, que basicamente podem ser: insuficiência de dados, erro de especificação do modelo (pode não ser uma reta), erro de especificação da variável explicativa (pode ter sido escolhida uma variável explicativa inadequada ou insuficiente para, sozinha, explicar a variabilidade de Y) ou fatores subjetivos / de difícil mensuração.

1 - Análise de Regressão com o auxílio do Excel

Inicialmente devemos verificar se nosso programa Excel está habilitado a executar uma análise de regressão. Para isso devemos clicar, dentro do programa, na guia Dados e verificar se o botão Análise de Dados está disponível:

Caso não esteja disponível o botão “Análise de Dados” teremos que configurar o Excel incluindo o suplemento de Análise de Dados. Para habilitar tal função, que é essencial para se desenvolver uma análise de regressão, deveremos clicar no botão Office , em seguida no botão Opções do Excel:

Na opção "Suplementos", clicar no Ir.

Em seguida, selecione a opção "Ferramentas de Análise" e confirme com o botão OK.

A partir daí poderemos desenvolver nossa análise de regressão. Para tanto deveremos digitar em nossa planilha os dados que iremos trabalhar. Para essa demonstração iremos adotar o mesmo exemplo já desenvolvido manualmente:

Para a determinação da equação e do coeficiente de determinação deveremos, após digitar os dados na planilha Excel, selecionar uma célula onde queremos que o resultado da análise apareça e depois, na aba Dados, clicar em “Análise de Dados”, selecionar a opção "Regressão" e clicar OK (conforme figura a seguir):

Deveremos clicar então nas pequenas setas vermelhas, que significam “entrada de dados” e selecionar os dados das variáveis independente “X” e dependente “Y”.

Deveremos, ainda, selecionar também através da pequena seta vermelha a célula que havíamos reservado anteriormente para a saída dos dados. Para que os dados já saiam na planilha final com os nomes das variáveis deveremos selecionar junto com os dados (números) as células com os próprios nomes das variáveis. Em contrapartida, para que o Excel entenda esse nosso procedimento deverá ativar o item “Rótulos”. Finalmente deveremos clicar em “ok” para que o Excel resolva as operações matemáticas de cálculo de nossa análise de regressão.

Essa função, ou seja, a análise de regressão com o auxílio do Excel irá fornecer vários resultados. Alguns destes não são objetos de nosso curso. Dessa maneira poderemos visualizar, em vermelho, os dados de nosso interesse nesse momento:

O coeficiente de determinação encontrado na análise de regressão com o auxílio do Excel “bateu” com o valor calculado manualmente de r2 = 0,966. Por outro lado os valos dos parâmetros “a” e “b” também “bateram” sendo iguais a “a” = 0,39 (já arredondado) e “b” = 69,69. É importante salientar que o valor desse parâmetro deu resultado um pouco diferenciado do resultado pelo cálculo manual (62,4) devido ao fato de que o Excel não arredonda os dados, o que culminou com essa pequena diferença. Se considerarmos no cálculo manual o valor do parâmetro “a” encontrado com três casas decimais, ou seja, 0,387, chegaríamos a um valor do parâmetro “b” igual a 69,72.

Resumo

Vimos anteriormente que a regressão linear é uma ferramenta importante para a análise de dados nos permitindo entender o relacionamento entre duas variáveis e fazer estimações.

Neste módulo apresentamos a realização da Análise de regressão utilizando a ferramenta "Análise de Dados" do Microsoft Excel. Para usar essa ferramenta precisamos habilitar o suplemento "Ferramentas de Análise". Uma vez habilitado temos acesso a diversas ferramentas de análise, dentre as quais a ferramenta "Regressão" que permite calcular com precisão os coeficientes a e b da regressão linear e dentre diversos outros parâmetros o coeficiente de determinação (R-Quadrado) que nos permite avaliar a aderência dos dados a esse modelo.