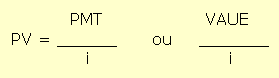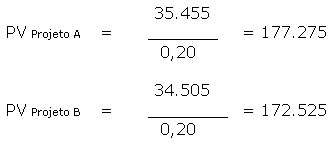1 - Reinvestimentos

Mais uma vez, continuamos a nos aproximar um pouco mais da realidade das grandes e médias empresas. O fato é que um projeto de alocação de recursos em ativos fixos, em geral, não é estanque e simples. Usualmente, com o passar do tempo, estes ativos necessitam nova alocação de recursos para a continuidade de suas produções.

É o caso, por exemplo, de bancos que, ao investir na abertura de uma agência (ativo fixo), necessitam periodicamente alocar recursos para sua manutenção, tais como pintura de paredes, atualização de hardware e software ou manutenção da rede elétrica.

A partir dos dados assumidos, o motorista de táxi monta o fluxo de caixa dos 6 anos, encontrando um fluxo de caixa de R$ 10.100,00 anuais.

Com base na taxa de juros de mercado vigente (10%a.a.), a projeção indica um Valor Presente Líquido (VPL) positivo de R$ 1.988 e uma Taxa Interna de Retorno (TIR) de 11,6%, indicando que seu projeto pessoal é viável e ele já pode deixar de trabalhar para a empresa e ser autônomo.

O veículo que será utilizado como táxi consome peças e pneus na geração de receitas. É necessário que, em algum momento ao longo dos seis anos, sejam feitos reinvestimentos na manutenção do seu ativo, caso contrário não se conseguirá gerar a receita prevista, seja porque o táxi não funcionará ou os clientes preferirão entrar em um táxi que lhes proporcione mais conforto e segurança.

Dessa forma, o motorista de táxi é alertado e, revendo suas projeções, chega à conclusão de que é necessário fazer uma revisão geral no terceiro ano, o que lhe consumirá R$ 1.800 em pneus e R$ 1.000,00 em peças.

Refazendo o fluxo, chega-se a um novo diagrama de projeto, cuja alteração ocorre no terceiro ano. Há, agora, uma previsão de reinvestimento no valor de R$ 2.800,00 que altera o resultado econômico do projeto.

Com base na taxa de juros de mercado vigente, que é de 10%a.a., a projeção indica agora um Valor Presente Líquido (VPL) negativo de R$116,00 e uma Taxa Interna de Retorno (TIR) de 9,9%, indicando que seu projeto pessoal não é mais viável.

Ou seja, todos os fatores que envolvem a projeção são importantes e necessitam ser muito bem mensurados, mas, sobretudo, necessitam ser muito bem mapeados.

O valor dos reinvestimentos é um fator tão importante quanto os fluxos de caixa gerados, o valor do investimento a ser feito, a vida útil do projeto e/ou a taxa mínima de atratividade.

Mas será mesmo? E se o motorista tiver se esquecido de um pequeno detalhe?

No entanto, na prática, não é isso que ocorre. Normalmente, os ativos possuem um valor de revenda no fim de sua vida útil contábil. Mesmo que pequeno ou simbólico, mesmo que só seja vendido como sucata, o ativo fixo pode, mesmo no fim de sua vida, possuir valor. Este valor é chamado residual.

Para entendermos como este método funciona na prática, vamos pegar como exemplo dois projetos, mutuamente excludentes, com os seguintes fluxos de caixa:

Supondo que a Taxa Mínima de Atratividade (TMA) é de 20%a.a., qual deveria ser o projeto escolhido? Em tese, bastaria calcular o Valor Presente Líquido de cada um dos projetos. O que apresentasse o maior VPL deveria ser o escolhido. Calculando-se o VPL dos projetos, temos o seguinte resultado:

Contudo, a avaliação fica bastante prejudicada em função dos prazos serem diferenciados. O fato de o Projeto B possuir um valor presente maior não significa que é o melhor projeto, pois possui um fluxo a mais que o Projeto A.

Enquanto o Valor Presente Líquido (VPL) demonstra o resultado líquido de um fluxo de caixa a valor presente, o VAUE evidencia um resultado equivalente em bases periódicas, como no caso citado, anual.

		130.000		210.000
VPL Projeto A = (200.000)	+	------------	+	-------------	=	54.167
		(1+0,2)1		(1+0,2)2

			80.000		130.000		200.000
VPL Projeto B =	(200.000)	+	--------	+	--------	+	--------	=	72.685
			(1+0,2)1		(1+0,2)2		(1+0,2)3

A solução desta questão ocorre com a utilização do VAUE. Este método consiste em obter um valor médio periódico equivalente dos fluxos de caixa positivos e compará-lo com valor médio dos fluxos de caixa negativos.

Uma das formas de se calcular o VAUE dá-se pela seguinte fórmula:

Para se calcular o VAUE basta utilizar as informações de cada fluxo mais o valor presente líquido calculado e o auxilio de uma calculadora financeira, dessa forma tem-se o seguinte resultado:

* Inverter o sinal utilizando a tecla CHS

O resultado calculado tem o seguinte significado: Projeto A apesar de possuir um valor presente líquido (VPL) menor que o Projeto B possui uma série uniforme periódica (no caso anual) maior que o projeto B.

Ou seja, o “VPL médio” do projeto A é melhor que o Projeto BEsta é a diferença entre o VPL e o VAUE. O VPL evidencia o resultado líquido do fluxo todo, enquanto o VAUE evidencia o resultado equivalente periódico (anual/mensal...) deste mesmo projeto.

É a mesma coisa no dia-a-dia das pessoas. Imagine que uma mãe oferece uma mesada para sua filha em duas opções:

a) 12 mensalidades de 100,00

b) 6 mensalidades de 150,00

Obviamente que, a princípio, o volume total da
primeira oferta é maior. Os R$1.200,00 é maior
que os R$900,00.

Contudo, a média mensal da primeira proposta é menor que a da segunda proposta. Enquanto a primeira proposta possui média de R$ 100,00 por mês a média da segunda é de R$ 150,00.

Obviamente que este exemplo é bem simples e a intenção é pura e simplesmente o entendimento sobre o conceito por trás do VAUE.

A mesma coisa podemos dizer sobre o projeto B. Os R$ 34.505 equivalem ao lucro médio por ano ao longo dos três anos de horizonte deste projeto.

Pode-se determinar o projeto que possui a média de fluxos periódicos mais interessantes de outra forma. Para tanto, deve-se determinar o mínimo múltiplo comum – MMC, entre os prazos das alternativas. É como se os fluxos fossem se renovando até um horizonte único. Ou seja, no exemplo anterior o MMC é igual a 6 (2 fluxo x 3 fluxos) para se igualar os respectivos horizontes. Depois, basta calcular-se o VPL como se fosse um projeto normal.

Montando-se os diagramas originais e os “projetados” visualiza-se mais facilmente o processo de se igualar os fluxos, como se eles se multiplicassem até o ponto de igualar seus horizontes.

Para se calcular o valor presente líquido dos projetos, o procedimento é o mesmo utilizado até então.

Para comprovar o cálculo do VAUE, basta achar o PMT (prestação) de cada um dos fluxos utilizando uma calculadora financeira, com base nos novos digramas projetados, ambos com horizonte de 6 anos, conforme o modelo:

* Inverter o sinal utilizando a tecla CHS

A conclusão é a mesma que a calculada pelo VAUE. Ou seja, se os projetos tivessem o mesmo horizonte o projeto A é melhor que o projeto B em função da média de seus fluxos de caixa anuais serem maiores.

• A primeira característica, como já abordado, é a diferença entre os horizontes. Reparem que no exemplo anterior um projeto possui 20 anos enquanto o outro apenas 5 anos.
• A segunda característica é derivada da primeira e diz respeito à perpetuidade destes projetos. No exemplo anterior assume-se que, caso não se faça benfeitorias no terreno, ele permanecerá cercado para o resto da vida. Isto quer dizer que o projeto de madeira deve ser “renovado” de cinco em cinco anos em função de sua vida útil.
  
  
  
  

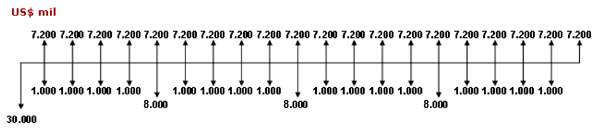
  Projeto Ano 00 Ano 01 Ano 02 Ano 03 Ano 04 Ano 05 Ano 06 Ano 07 Ano 08 Ano 09 Ano 10 Ano 11 Ano 12 Ano 13 Ano 14 Ano 15 Ano 16 Ano 17 Ano 18 Ano 19 Ano 20 Concreto (12.500) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) (1.250) Madeira (6.200) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100) (2.100)

Dessa forma, para se decidir pelo melhor projeto deve-se, necessariamente, utilizar a metodologia do Valor Anual Uniforme Equivalente – VAUE.

Calculando-se o VAUE dos projetos do exemplo anterior, temos o seguinte resultado:

(**) Não é necessário inverter o sinal em função do projeto já apresentar VPL negativo. Lembrar que o projeto é apenas de fluxos negativos e, apesar da calculadora financeira apresentar PMT positivo, o valor refere-se a prestações negativas.

O resultado do exemplo indica que é preferível o projeto de cerca de concreto em função de este material proporcionar fluxos de caixa negativos (custos) médios menores que o projeto de cerca de madeira.

1 - Perpetuidade

Estes conceitos serão utilizados a todo o momento e são indispensáveis para o entendimento dos conceitos a serem estudados.

A perpetuidade é um destes conceitos avançados que podemos utilizar em muitas das análises de projetos de investimentos fixos. Como abordado no conteúdo do VAUE, muitos projetos tem horizontes de vida diferentes e em muitos casos os projetos tendem a se perpetuar.

É o caso, por exemplo, da abertura de uma empresa ou filial de uma empresa. Ninguém faz um investimento pensando em fechar as portas no ano seguinte. Para estes casos, ao invés de se ficar calculando indicadores sobre fluxos intermináveis, pode-se utilizar o conceito de perpetuidade.

A perpetuidade é derivada do VAUE e consiste em achar o VPL após o período explícito de crescimento.

Sendo assim pode-se calcular o Valor Presente Líquido (VPL) de cada uma das alternativas /projetos por meio da fórmula utilizada para séries infinitas, a saber:

Vamos voltar ao exemplo utilizado quando da análise do VAUE.

Calculando-se a perpetuidade dos projetos temos:

Portanto, a primeira alternativa é a mais viável, pois, assim como o VAUE, apresenta um VPL maior.

Refletindo um pouco sobre a origem desse cálculo, sem os rigores das formulações matemáticas, pode-se pegar o comportamento do Valor Presente Líquido de um projeto, dada determinada taxa de juros, conforme gráfico abaixo:

Notamos, neste gráfico, que o VPL aumentará à medida que se aumenta o prazo, mas não de forma constante. Independente da taxa de desconto utilizada, essa curva é mais ascendente nos primeiros anos e suave e insignificante ao longo tempo.

2 - Ponto de Equilíbrio

Contudo, para entendermos a importância e o cálculo do ponto de equilíbrio de forma mais apropriada, é vital revisar alguns conceitos contábeis relativos a custos.

Os custos podem ser classificados de várias formas em função da análise que se quer fazer. Para a finalidade de análise do ponto de equilíbrio, os custos devem ser divididos em fixos e variáveis.

Custos - Custos podem ser definidos como os gastos relativos a bens e/ou serviços utilizados na produção de outros bens ou serviços. O custo é reconhecido no momento da utilização de fatores de produção necessários para a fabricação de um produto ou execução de um serviço.

Os custos variáveis são aqueles que mudam de acordo com o volume de produtos ou serviços produzidos dentro de uma unidade de tempo. Dessa forma, pode-se representar o comportamento do custo variável de acordo com o gráfico abaixo:

Percebam que à medida que o volume aumenta o custo se eleva proporcionalmente.

O crescimento do custo, assim como o da receita são lineares e uniformes, em função de ambos crescerem diretamente. O aumento do resultado se dá em decorrência do aumento da produção.

Perceba que apesar de contínuo o comportamento do custo fixo pode se alterar em degraus caso haja necessidade de se alterar limites de produção, por exemplo.

São exemplos clássicos de custos fixos: depreciação das máquinas, aluguel e impostos prediais, mão de obra indireta utilizada na produção tal como um vigia noturno e contas de telefones da fábrica dentre muitos outros.

As empresas incorrem invariavelmente nos dois tipos de custos para produzirem seus produtos e a gestão de ambos é fator preponderante para o sucesso. A conjunção dos dois, forma o custo total de uma empresa assim como de um novo empreendimento ao qual se deseja alocar investimentos.

A finalidade da classificação dos custos em fixos e variáveis é que esta permite uma melhor comparação entre alternativas de projetos com diferentes estruturas de custos.

Assim, pode-se verificar qual a melhor alternativa para diferentes níveis de produção ou demanda.

Break even point ou o ponto de equilíbrio propriamente dito pode mostrar o nível de atividade a partir do qual um negócio/projeto se torna lucrativo ou, nos casos dos projetos de investimentos, viável.

A princípio, a análise do ponto de equilíbrio está sempre associada à idéia de identificar o volume mínimo de produção (vendas) que permita cobrir custos fixos e custos variáveis.

Perceba que, até então, as metodologias estudadas prestam-se às análises quanto à viabilidade dos projetos por meio do estudo do retorno dos investimentos efetuados. Em nenhum momento considera-se o mérito dos valores mínimos, seja de receita ou quantidade de produtos/serviços vendidos requeridos para se garantir a viabilidade de um projeto. As análises também não se preocupam com o nível das despesas e com a margem de contribuição mínima necessária ao atingimento da viabilidade econômica financeira.

No caso da Análise de Investimentos, a idéia do ponto de equilíbrio é identificar os volumes mínimos necessários da variável considerada mais crítica sob o ponto de vista do projeto de investimento.

Vamos utilizar o seguinte exemplo:

Apesar de haver muitas informações neste exemplo, é necessário apenas trabalhar de forma ordenada e em etapas, utilizando os conceitos até agora estudados, para resolver a questão e analisar o caso.

Por fim a receita prevista ocorrerá em função do fluxo de 10.000 veículos que trafegarão na rodovia por dia e que pagarão pedágio no valor de US$2,00. Considerando o ano normal com 360 dias tem-se uma receita prevista de US$7.200.000 (10.000 x 360 x 2,00).

A montagem do diagrama de fluxo de caixa ajuda a visualizar o projeto de forma mais clara e auxilia a interpretação do problema. De acordo com as informações levantadas na etapa anterior temos as informações quanto ao investimento, receitas e custos e, dessa forma, pode-se evidenciá-las conforme mostra o quadro abaixo:

3ª etapa – Calcular os indicadores de retorno e viabilidade

Antes de aprofundarmos a análise sobre o ponto de equilíbrio, é necessário, a partir da construção do fluxo caixa projetado do negócio, calcular os indicadores de viabilidade conforme metodologias estudadas até aqui.

Indicadores
VPL = R$ 2.798.163,93
TIR = 16,74% a.a.

Portanto, o custo máximo admitido são os fluxos de caixa negativos trazidos a valor presente no montante de R$32.798.163,93.

A margem de segurança, que é uma medida de risco, pode ser calculada pela relação entre a folga e o valor presente dos fluxos de saída.

Esta taxa significa dizer que os custos só podem crescer 9,33% para que o projeto ainda continue viável, caso contrário, o projeto de investimento torna-se inviável. Para comprovar, basta multiplicar os mesmos R$ 30.000.000 pela taxa de 9,33%, e serão encontrados os mesmos R$ 2.798.163,93.

b) O ponto de equilíbrio é calculado com base no mesmo raciocínio. Neste caso, a lógica também é simples. Tomemos novamente o conceito de ponto de equilíbrio. O break even point é o ponto em que as receitas cobrem os custos e o resultado contábil da empresa é nulo. Dessa forma, no fluxo de projetos de investimentos basta igualar o valor presente líquido das saídas (custos/despesas) ao valor presente líquido das entradas.

Calculando-se o VPL das saídas, encontra-se o valor de R$ 42.269.022,68. Para “zerar” este valor deve-se achar a receita anual que, a uma taxa de 15%a.a., faça com que o VPL das entradas proporcione os mesmos R$ 42.269.022,68 e o VPL do projeto, conseqüentemente, seja nulo.

VPL saída = VPL entrada

Utilizando-se a calculadora financeira, basta inserir as informações para encontrar a prestação anual – PMT (receita anual), seguinte forma:

* Inverter o sinal utilizando a tecla CHS

Analisando este resultado, pode-se compreender que, se a rodovia gerar uma receita de US$ 6.752.961,22 por ano, o valor presente líquido do projeto será nulo.

Outra interpretação que se pode dar é que esta receita anual calculada é a receita mínima exigida para se diluir todos os custos existentes sem prejudicar a viabilidade, pois o resultado será nulo.

Calculando a receita, pode-se ainda descobrir o ponto de equilíbrio em quantidade de veículos. Para tanto, basta dividir a receita anual de equilíbrio pela quantidade de dias (360). Daí, divide-se o resultado encontrado pelo valor da tarifa que é de US$ 2,00.

Esta taxa calculada significa dizer que a quantidade de veículos só pode variar, para baixo, em 6,2089%, caso contrário, o projeto tornar-se-á inviável.

Até este momento, foram vistos muitos conceitos básicos e elementares para se proceder a uma análise de projeto de investimentos em ativos fixos.

A perpetuidade é um conceito que pode ser utilizado em muitas das análises de projetos de investimentos fixos. Derivado do VAUE a perpetuidade deve ser utilizada em projetos cujo horizonte de vida tende a se perpetuar.

É o caso, por exemplo, da abertura de uma empresa ou filial de uma empresa. Ninguém faz um investimento pensando em fechar as portas no ano seguinte.

A princípio, a análise do ponto de equilíbrio está sempre associada à idéia de identificar o volume mínimo de produção (vendas) que permita cobrir custos fixos e custos variáveis.

O ponto de equilíbrio, ou break even point como também é conhecido, é o ponto em que as receitas cobrem os custos e o resultado contábil da empresa é nulo e refere-se ao estudo dos pontos mínimos e máximos aceitáveis de receitas e custos, respectivamente, a fim de dimensionar os riscos de inviabilidade dos projetos de investimento.

1 - Taxa Mínima de Atratividade Ajustada

Quaisquer que sejam os tipos de taxas de juros conhecidas no mercado, todas exprimem, em essência, a remuneração pela alocação de capital.

A taxa de juros reflete, portanto, o preço pelo sacrifício de poupar, o que equivale, em outras palavras, à remuneração exigida por um agente econômico ao decidir postergar o consumo, transferindo seus recursos a outros agentes.

As taxas de juros que precificam os ativos do governo no mercado é denominada taxa livre de risco, constituindo-se na taxa base do sistema econômico.

Por outro lado, a taxa de juros vigente na economia pode assumir diversos valores de acordo com o risco oferecido pelas diversas alternativas financeiras.

Portanto, a taxa de juros base de uma economia é a taxa mínima, estando sempre abaixo dos retornos oferecidos pelos ativos que não sejam títulos governamentais. Em contrapartida, a taxa de juros estabelecida livremente pelo mercado é a taxa referencial a ser comparada com os retornos oferecidos pelos investimentos com risco.

A taxa de juros (prefixada) de um ativo ou mais comumente conhecida como taxa mínima de atratividade pode ser explicada com base em quatro componentes:

A taxa mínima de atratividade pode e deve ser ajustada para compensar o fato de a empresa estar assumindo um risco maior ou menor, conforme o caso.

Este ajuste na taxa é uma forma prática e direta de se ajustar o projeto à clara exposição às oscilações de fluxos existentes. É necessário ter em mente que as projeções até então vistas são de caráter determinístico e seguem princípios de conservadorismo. Dessa forma, nada melhor que um ajuste na taxa para evidenciar um potencial risco.

Exemplo:
O Banco Zeta Ltda. está estudando a ampliação de sua base de rede de agências, pretendendo dobrar sua capacidade de atendimento.

Alternativamente, há possibilidade de inaugurar uma nova modalidade de canal de atendimento cuja característica difere bastante das tradicionais que é através da telefonia móvel. Os fluxos de caixa associados aos dois estudos são os seguintes:

O canal tradicional de atendimento é bem conhecido com uma série histórica de resultados bem consistente. Sua taxa mínima de atratividade é de 12% a.a..

Calculando-se o valor presente líquido (VPL) e o valor anual uniforme equivalente (VAUE) tem-se:

Percebe-se que o novo canal de relacionamento, representado pela telefonia móvel, possui um retorno traduzido pelo indicador VAUE muito maior que o canal tradicional, aqui representado pelo universo das agências.

Contudo, o Banco Zeta Ltda. decide por analisar este novo mercado de forma um pouco mais detalhada e evidencia um nível de risco bem maior em função dos números de fraude, a velocidade da evolução tecnológica e a maturidade do mercado.

Em função disto, decide adicionar 8 pontos percentuais à taxa mínima de atratividade deste projeto, que passa a ser 20%a.a.. Desta forma os indicadores se alteram de acordo com tabela e gráfico abaixo:

Apesar da grande redução de 56,6% no VAUE do projeto do canal alternativo telefonia celular, referente ao valor de US$ 22.833 para US$ 9.910, o projeto ainda se mostra mais viável que o projeto de canal tradicional que possui um VAUE de apenas US$ 2.979.

A redução ocorreu em função do incremento de 8 pontos percentuais feito na taxa de desconto, devido à percepção do maior risco envolvido no novo negócio.

O importante é entender que os indicadores que mensuram a viabilidade dos projetos se alteram à medida que o fator de risco é inserido à taxa de desconto do projeto. No caso acima, mesmo compensando a taxa mínima de atratividade do projeto de canal alternativo com 8 pontos percentuais a mais, seu VAUE continuou maior evidenciando realmente ser a melhor alternativa.

2 - Análise de Sensibilidade

Atenção usar cores do padrão

A análise de sensibilidade é ferramenta importantíssima para as empresas e seus analistas, principalmente quando da análise de investimentos projetados de forma determinística e não probabilística.

É importante reiterar que esta técnica é utilizada normalmente em situações em que não há quaisquer informações sobre a distribuição de probabilidades e consiste, basicamente, na avaliação de risco de volatilidade dos indicadores de retorno de projetos, principalmente o VPL, em função de possíveis variações das premissas que fundamentam sua projeção.

Em outras palavras, a técnica procura medir o efeito da possível oscilação em uma determinada variável, sobre a rentabilidade de um projeto. Para estes casos, costuma-se admitir variações naqueles itens, ou conjunto de itens, nos quais há maior incerteza nas previsões.

Quando há pequena variação num parâmetro o qual altera drasticamente os resultados esperados, diz-se que o projeto em análise é muito sensível a esse parâmetro e poderá ser interessante concentrar esforços para obter dados menos incertos.

De forma direta, a análise de sensibilidade procura responder perguntas do tipo “O que aconteceria com os indicadores do projeto em estudo, se variássemos determinado parâmetro?”. As suposições poderiam ser até extremistas e isso ajudaria o decisor a identificar o grau de sensibilidade dos parâmetros componentes da projeção.

Exemplo:
A empresa petroquímica Limitada Ltda. estuda a possibilidade de lançar um novo produto no mercado. O Tetra tri penta – B é um produto inovador que atenderá o segmento de semicondutores. Para tanto, foram projetados os seguintes dados para estudo de sua viabilidade.

Investimento – Equipamento US$ 40.000
Investimento – Capital de Giro US$ 2.000
Receita projetada US$ 20.000
Custo da matéria prima US$ 4.000
Custo da mão de obra US$ 2.000
Vida útil (anos) 5 anos
TMA 10%a.a.

Montando-se o diagrama do fluxo deste projeto, tem-se a seguinte situação:

A projeção básica indica que o projeto de investimento é viável, pois possui um valor presente líquido positivo de US$ 11.071.

Mas, e se alguns dos valores das premissas sofressem algum tipo de flutuação?

Simulando-se algumas variações nas premissas, isoladamente, pode-se analisar a sensibilidade do VPL e da TIR do projeto em relação a estas alterações. Para efeitos de entendimento, serão construídas cinco simulações. Para melhor acompanhamento os valores alterados aparecem em negrito.

Analisando quadro-resumo abaixo, percebe-se que somente na ocorrência do pior dos cenários possíveis, que é a ocorrência simultânea de todas as variações simuladas, é que o projeto torna-se inviável.

Ferramentas - Uma das ferramentas mais acessíveis para auxiliar o processo de análise de sensibilidade são as planilhas eletrônicas Excel.

O processo pode ser feito por meio de formatação de fórmulas básicas ou, também, por meio de funções avançadas como a utilização de solvers e tabelas.

Atingir metas - Essa é uma função simples e útil na simulação de uma situação em que se deseja atingir determinado valor como meta. Esta função é indicada na solução de problemas em que se deseja atingir uma única meta, pela variação de uma única variável.

Um exemplo típico é o de calcular-se o valor de investimento máximo permitido de um projeto para que o VPL seja nulo, em função de uma projeção de fluxo de caixa.

Exemplo:

O Sr. Lee Oswald, proprietário do carrinho de cachorro quente Cold dog, pretende abrir uma nova “filial” do seu negócio na rodoviária da cidade. Ele passa o dia no local, contando quantas pessoas transitam pelo ponto onde pretende instalar seu novo carrinho. De acordo com seus cálculos consegue-se vender 10.000 cachorros quentes a um preço de R$ 2,00. Sabendo-se que o custo de cada cachorro quente é R$ 1,05, a vida útil do carrinho é de 4 anos e a taxa mínima de atratividade é de 15%a.a., qual o valor de investimento máximo para que o projeto seja viável ao final de 4 anos.

Após o primeiro passo, que é a disposição dos dados de forma ordenada na planilha eletrônica, com suas respectivas fórmulas de somas e cálculos de porcentagens, aciona-se a função Ferramentas para então acionar-se a função Atingir Metas.

O que se quer calcular é o investimento máximo (Valor do investimento) para que o projeto seja viável. Ou seja, qual o investimento máximo cujo VPL seja nulo ou zero. Portanto, a terceira informação será a célula cujo valor se quer calcular e que, no caso, é o investimento máximo.

Solver - é uma extensão de a função atingir metas, mas com uma capacidade maior para processamento de variáveis. Como objetivo principal pode-se estabelecer não apenas um valor definido, mas também metas como maximizar ou minimizar o resultado de determinado problema.

Vejamos um caso clássico de utilização de solver. Exemplo:

O Sr. Lee Oswald vende 2 produtos em seus carrinhos de cachorro quente. O primeiro é o próprio hotdog que possui uma margem de contribuição, como visto no problema anterior, de R$ 1,05. O outro produto é um refresco, cuja margem de contribuição é de 0,75.

Para vender um cachorro quente são necessários 5 minutos para montagem do sanduíche, enquanto que a venda do refresco consome apenas 2 minutos. Em compensação, o consumidor de cachorro quente permanece em média apenas 2 minutos na cadeira enquanto que o consumidor do refresco fica sentado por 4 minutos.

Sabendo-se que o dia tem uma capacidade limite de 8 horas ou no caso 480 minutos, qual é a composição entre os produtos que maximiza a margem de contribuição?

O primeiro passo é dispor os dados de forma ordenada na planilha eletrônica com suas respectivas fórmulas.

Em seguida, acionam-se as funções Ferramentas e Solver. Daí preenche-se o quadro parâmetros do Solver conforme abaixo:

Surge, também, um quadro para emissão de relatórios especiais de Respostas, Análise de Sensibilidade e de Limites das variáveis envolvidas no problema, bem como a opção para salvar a simulação.

Perceba que a quantidade de produtos a ser vendidos que maximiza a margem de contribuição da empresa, em função da margem unitária e do tempo de preparação dos produtos e permanência do cliente, é 30 cachorros quentes e 45 refrescos.

Dessa forma, o Solver é uma ferramenta complementar e fundamental para auxiliar as empresas e os analistas de projetos de investimento na construção de sistemas para otimizar resultados, minimizar custos e atingir metas essenciais à viabilidade dos projetos.

Resumo

Quaisquer que sejam os tipos de taxas de juros conhecidas no mercado, todas exprimem, em essência, a remuneração pela alocação de capital.

A taxa de juros reflete, portanto, o preço pelo sacrifício de poupar, o que eqüivale, em outras palavras, à remuneração exigida por um agente econômico ao decidir postergar o consumo, transferindo seus recursos a outros agentes.

Uma forma de se mensurar o risco de um projeto é por meio da Taxa Mínima de Atratividade. Uma vez levantados os riscos inerentes ao negócio ou ao projeto, é possível inserir na TMA um fator de diferenciação necessário à comparação de projetos que normalmente são distintos.

Outro instrumento importante na avaliação de riscos das projeções é a análise de sensibilidade, principalmente quando os projetos têm caráter determinístico e não probabilístico.

Esta técnica procura medir o efeito da possível oscilação em uma determinada variável, sobre a rentabilidade de um projeto. Para estes casos costuma-se admitir variações naqueles itens, ou conjunto de itens, onde há maior incerteza nas previsões.

Costuma-se utilizar, para tanto, o auxílio de calculadoras financeiras, quando o projeto é pequeno e simples, ou planilhas eletrônicas cujas funções são mais potentes e flexíveis, tal como a função Solver.

1 - Inflação

O processo inflacionário, presente numa economia, pode causar impactos nos relatórios contábeis das empresas e, de certa forma, nas análises dos projetos de investimentos em ativos e suas respectivas viabilidades econômico-financeiras.

A influência inflacionária nas diversas atividades exercidas por qualquer empresa induz o administrador financeiro à necessidade de dar maior atenção ao fenômeno.

Para entender um pouco mais claramente o conceito de inflação, vamos tomar um exemplo bem simples. Exemplo.

Índice Geral de Preços no Mercado - IGP-M - Também calculado pela Fundação Getúlio Vargas, apresenta amplas aplicações no mercado. A principal diferença verificada entre esse índice e o IGP-DI reside no período da medição da inflação. No IGP-M, a taxa de inflação medida cobre o período compreendido entre o dia 11 de um mês e o dia 10 do mês posterior. As demais características do IGP-M são iguais ao IGP-DI, sendo que a cada dez dias são divulgadas prévias do resultado do mês, permitindo que o mercado se antecipe à taxa de inflação do mês.

Índice Nacional de Preço ao Consumidor - INPC

O INPC reflete, pelos percentuais publicados todo mês pelo Instituto Brasileiro de Geografia e Estatística (IBGE), de maneira parcial, a evolução da taxa de inflação da economia, medida pelos IGPs apresentados.

A explicação principal desse comportamento parcial é o fato de o INPC referenciar a evolução dos preços somente com base em bens e serviços destinados ao consumo, não computando bens intermediários e de capital. A aplicação desse índice recai preferencialmente sobre os reajustes salariais. O levantamento dos preços é efetuado mensalmente, com base em uma cesta de consumo de famílias com renda de 1 a 8 salários mínimos.

Pode-se perceber que são poucas as diferenças entre estes três indicadores e que suas curvas ao longo de 16 anos evidenciam esta semelhança.

Existem outros indicadores no mercado com diferentes formações e periodicidades, criados para determinados setores da economia. É o caso do INCC (índice Nacional da Construção Civil)

2 - Decisões de Investimentos e a Inflação

Nas técnicas de avaliação de investimento, tradicionalmente, supõe-se que todos os preços e custos envolvidos no estudo se elevarão de forma proporcional. Portanto, o efeito de uma variação nos valores monetários envolvidos seria nulo.

Como foi estudado, uma empresa quando elabora um projeto de investimento está na realidade esperando obter um retorno sobre seu capital aplicado, que seja superior à taxa de desvalorização da moeda, isto é, uma taxa real.

Inflação constante ao longo do tempo - Admitamos, inicialmente, que a inflação é constante e atinge igualmente todos os preços e custos envolvidos. Neste caso, a inflação não alterará o resultado e a decisão final, pois todos os componentes sofrem a influência da taxa da inflação simultaneamente.

Exemplo:

Uma empresa estuda investir em um equipamento no valor de R$ 10.000, o que produzirá um resultado líquido de R$ 4.200 por ano durante três anos. A empresa tem expectativa de taxa mínima de retorno (TMA) de 10% a.a. acima da inflação. O fluxo de caixa possui a seguinte estrutura:

Montando-se o diagrama do projeto e calculando-se o VPL e a TIR descontado, a uma taxa de 10%a.a., tem-se:

Contudo, a empresa considera que a inflação nos próximos 3 anos está estimada em 30%a.a. e é aplicável a todos os fatores. Neste caso, será que o projeto continua aceitável?

Remontando-se a tabela com os novos valores corrigidos, reconstruindo-se o diagrama do projeto e calculando-se o VPL e a TIR a uma taxa de 43%a.a. (TMA + Inflação) têm-se:

Nota-se que o VPL é o mesmo que o projeto anterior. Isto porque, apesar das varáveis do projeto terem sofrido um reajuste com base na inflação, a taxa de desconto também continha a inserção da taxa da inflação. Desta maneira uma anulou a outra.

Contudo, como explicar a TIR de 46,28%, bem acima dos 12,5% do projeto original. É necessário lembrar que a metodologia TIR possui alguns problemas, dentre os quais, não considerar a taxa mínima de atratividade no seu cálculo, mas, sim, apenas seus próprios fluxos.

Então, é fato que, como os fluxos forma inflacionados, a TIR também. Dessa forma, ao extirpar-se a inflação do período da taxa interna de retorno, utilizando a equação de Fisher tem-se:

Portanto, deve ter ficado claro que o fato de incluir ou não a inflação nos fluxos de caixa, de forma homogênea, não altera a decisão quanto à aceitação ou rejeição do projeto. O impacto da inflação, quando atingem todas as variáveis simultaneamente, não afeta o projeto, tampouco sua viabilidade.

Variação nos preços relativos - Em países com elevada taxa de inflação, há uma tendência a variações nos preços relativos dos produtos e insumos. O Brasil já viveu uma era, até o início da década de 1990, de altos níveis de inflação, quando as taxas atingiam patamares superiores a 50% ao mês.

Apesar de o país viver uma fase de estabilidade econômica e inflacionária, o raciocínio a ser apresentado também é factível para patamares de inflação reduzidos.

Imagine que a mesma empresa do exemplo anterior tenha feito uma análise mais aprofundada do seu projeto e do impacto da inflação sobre suas variáveis e tenha constatado que a taxa de inflação é constante ao longo do tempo, mas afeta cada item diferentemente, conforme é mostrado abaixo:

Será que o projeto continuará possuindo o mesmo VPL e TIR?

Projetando-se cada parâmetro com base na taxa de inflação de cada um, obtém-se:

Montando-se o diagrama deste projeto e descontando-o a 43% ao ano (TMA + Taxa de inflação), tem-se:

Na prática, o que se fez foi corrigir todos os preços e custos pela inflação específica esperada para cada um dos componentes do projeto e transformar o fluxo de caixa resultante, expresso em preços correntes, para um fluxo de caixa em preços constantes.

Ao conseguir mensurar estas variáveis é possível alocar os incrementos ou reduções, assim como foi feito com a inflação.

3 - Sistemas de Amortização

O sistema de amortização trata, basicamente, da forma com que um agente devedor pode saldar suas dívidas, segundo regras ou acordos estabelecidos entre as partes de sistemas convencionais de amortizações.

Não importa o plano ou sistema de amortização adotado numa operação, pois, como são regidos pelo sistema de juros compostos e os juros são sempre calculados sobre os saldos devedores, os planos serão sempre equivalentes.

Sistema Francês

Como o próprio nome indica, nesse sistema as prestações são constantes e correspondem a uma série uniforme.

Sua fórmula matemática é dada pela seguinte equação:

Obviamente, pode-se utilizar também uma calculadora financeira como procedemos durante todo o curso.

* Inverter o sinal utilizando a tecla CHS

Neste sistema, a parcela de juros decresce com o tempo, ao passo que a parcela de amortização aumenta com o tempo. Graficamente, pode-se apresentar este comportamento da seguinte maneira:

Montando-se a planilha de acompanhamento do Saldo devedor (do exemplo citado anteriormente):

Sistema de Amortização Constante – SAC - Esse sistema foi popularizado pelo Sistema Financeiro de Habitação (SFH), que o adotou nos financiamentos de compra da casa própria. Atualmente, ele é muito utilizado para financiamentos no longo prazo. Como as amortizações são constantes, seu valor é obtido dividindo-se o principal (PV) pelo número de prestações (n). Portanto, dessa forma, a primeira prestação (amortização + juros) será maior que a segunda, pois os juros começam a cair simultaneamente com a base de cálculo (saldo devedor).

Neste sistema, a parcela de juros decresce com o tempo, ao passo que a parcela de amortização permanece fixa. Graficamente, pode-se apresentar este comportamento da seguinte maneira:

Resumo

A inflação é um processo de desvalorização da moeda dado pela corrosão da moeda de uma Nação. Ela afeta sobremaneira as empresas e pode ser diferente de entidade para entidade, em função dos recursos que são utilizados na execução de suas atividades.

O processo inflacionário presente numa economia causa impactos nas empresas, que são refletidos em seus relatórios contábeis. Além disso, podem afetar também as projeções e análises de alocação em capital fixo, As decisões quanto à viabilidade econômico-financeiras dos projetos de investimentos em ativos e suas respectivas viabilidades.

A influência inflacionária nas diversas atividades exercidas por qualquer empresa induz o administrador financeiro à necessidade de dar maior atenção ao fenômeno.

Outro aspecto importante a ser estudado são os sistemas de amortização utilizados pelo Sistema Financeiro com suas características e diferenças. O comportamento dos juros e das amortizações em cada modalidade varia, mas o produto final, basicamente, é o mesmo, em vista de todos trabalharem com o Sistema de Capitalização de Juros Compostos.