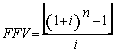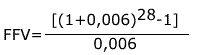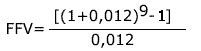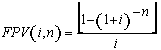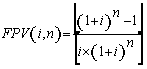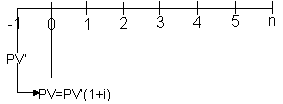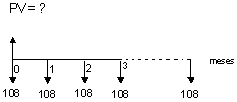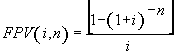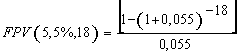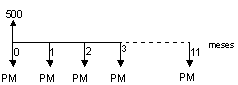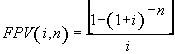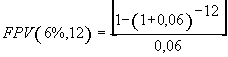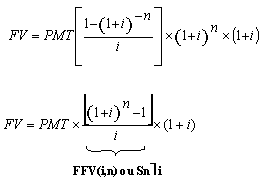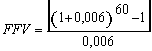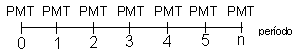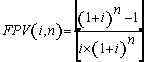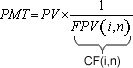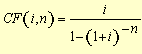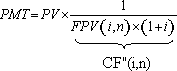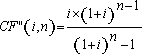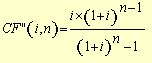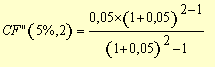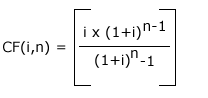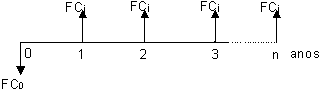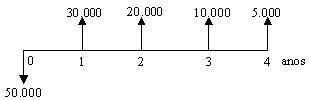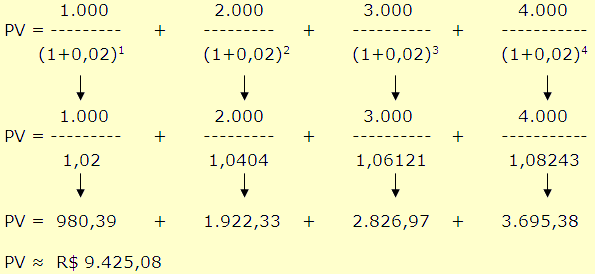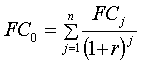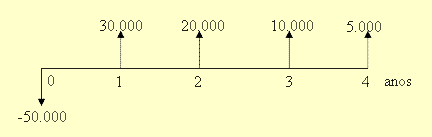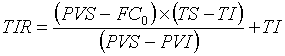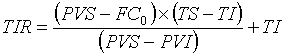|
1) Qual
será o preço à vista de uma mercadoria adquirida
em 18 parcelas iguais e sucessivas, no valor de R$ 108,00, sabendo-se
que a primeira parcela ocorre no ato da compra e que a taxa de juros do
financiamento é de 5,5% a.m.?
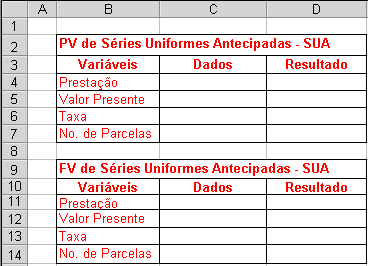
Importante!
Sempre que se tratar de uma “SUA”, o problema irá indicar
a ocorrência da primeira parcela: “na data atual”, “hoje”,
“no momento da compra” etc.
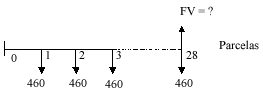
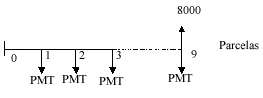
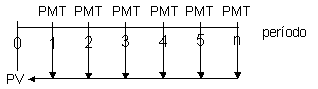
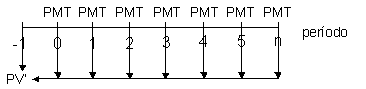
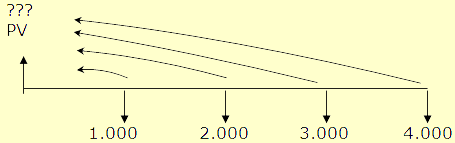
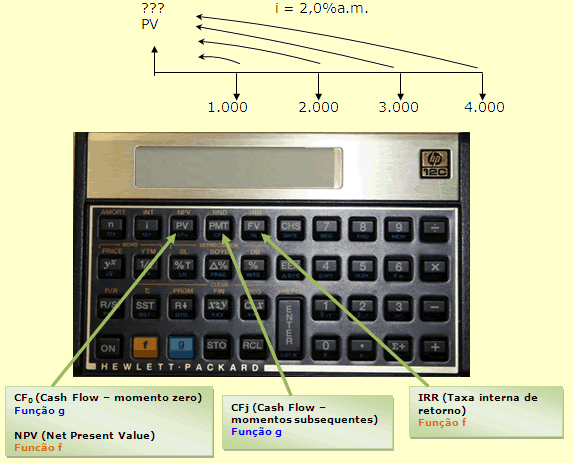
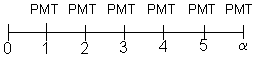
Fluxo:
O valor presente
de R$ 1.281,38 poderia ser encontrado se descapitalizássemos os
fluxos um a um e depois somássemos o resultado.
Observação:
Para qualquer série antecipada, com taxa igual a 5,5% e número
de termos igual a 18, o fator de valor presente (FPV(5,5%,18)) será
igual a 11,246074.
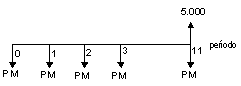
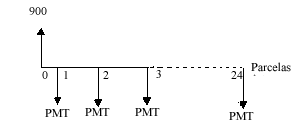
2) Uma loja
anuncia a venda de um eletrodoméstico, no valor de R$ 500,00, em
12 prestações, iguais e sucessivas, a primeira ocorrendo
no ato da compra. Considerando que a taxa de juros da operação
é de 6% a.m., calcular o valor das prestações.
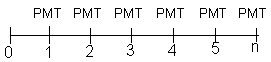
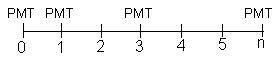
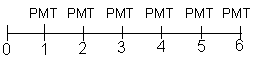
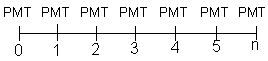
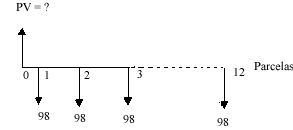
Fluxo:
|
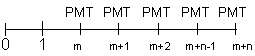
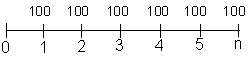
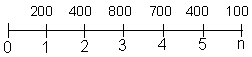

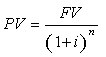
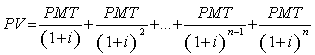
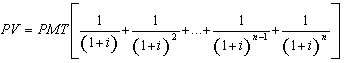
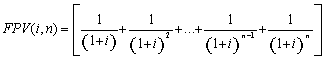
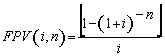
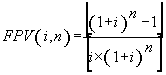
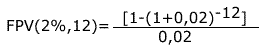
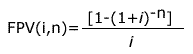
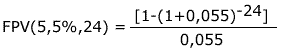
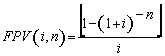 (7), substituindo-se FPV (i,n) da expressão (7) na fórmula
(10) e resolvendo a equação teremos:
(7), substituindo-se FPV (i,n) da expressão (7) na fórmula
(10) e resolvendo a equação teremos: