Torna-se importante frisar que, em virtude do fato de haver somente um operador na equação, pode-se fazer também uma avaliação da equação dividindo-a em pares. Para melhorar o entendimento vamos supor que primeiramente vamos achar o resultado de A+B, para então operar os valores resultantes com os respectivos valores de C. Esta propriedade é conhecida como associativa. A ordem das variáveis não é importante em virtude da propriedade comutativa, sendo assim a ordem em que são avaliadas as variáveis A, B e C é irrelevante. Estas propriedades são visualizadas pela tabela verdade abaixo. Nesta tabela, os parêntesis servem para indicar as subexpressões que já foram avaliadas na coluna imediatamente à esquerda.
Você deve ter observado que os valores das colunas referentes às expressões A+B+C, (A+B)+C e (B+C)+A são os mesmos (na mesma ordem).
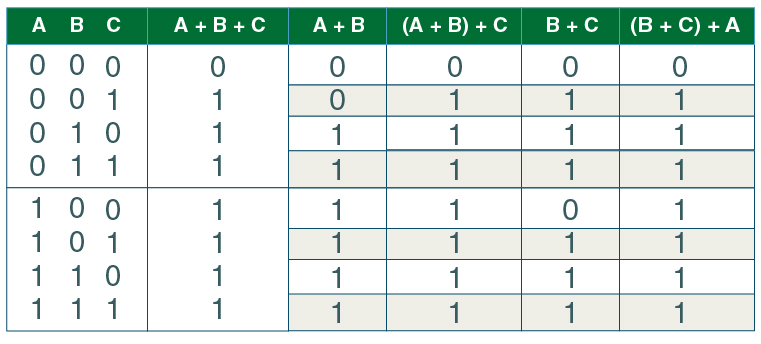
Propriedade associativa
Quer dizer que, ao associarmos algumas parcelas, o total fica inalterado. No conjunto dos números naturais, a adição é associativa, isto é, é possível associar as parcelas de quaisquer modos, ou seja, com três números naturais, somando o primeiro com o segundo e ao resultado obtido somarmos um terceiro, obteremos um resultado que é igual à soma do primeiro com a soma do segundo e do terceiro.
Exemplo:
(2 + 3 ) + 4 = 2 + ( 3 + 4 ) = 9
XPropriedade comutativa
Quer dizer que a ordem das parcelas não altera a soma. No conjunto dos números naturais, a adição é comutativa, pois a ordem das parcelas não altera a soma, ou seja, somando a primeira parcela com a segunda parcela, teremos o mesmo resultado que somando a segunda parcela com a primeira parcela.
Exemplo:
2 + 6 = 6 + 2 = 8
X