Resumo

Com o emprego de um ou mais conectivos é possível compor um pensamento novo. Cada conectivo original uma operação da lógica das proposições e, por sua vez, cada operação possui uma regra própria de interpretação. Assim, para a interpretação final de uma proposição, deve-se identificar o conectivo em análise e aplicar a respectiva regra.

Sumarizando o entendimento de cada regra, a tabela a seguir traz a situação que conduz ao resultado V (Verdade) na interpretação das operações lógicas Condicional, Bicondicional e Negação, separadamente:

Operação Lógica				Quando é verdade?
p→q	"Se-então"	Condicional	Relação de inclusão p ⊂ q	Só é falso quando V→F. É verdade nos demais casos.
p↔q	“se somente se”	Bicondicional	Relação de igualdade p = q	Quando p e q possuem valores lógicos iguais.
~p	"não"	Negação	Relação de complemento (de inverso)	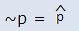Quando p é falso.

Para o estudo da lógica das proposições é necessária e obrigatória a compreensão dessas e das demais operações lógicas, que foram consolidadas na tabela abaixo:

Operações Lógicas		Quando é verdade?
p∧q	Conjunção	Quando ambos são verdade.
p∨q	Disjunção	Quando pelo menos um dos dois for verdade.
p⊻q	Disjunção exclusiva	Quando apenas um dos dois é verdade.
p→q	Condicional	Só é falso quando Vp→F. É verdade nos demais casos.
p↔q	Bicondicional	Quando p e q possuem valores lógicos iguais.
~p	Negação	Quando p é falso.

Clique no botão ao lado para baixar a tabela acima: Baixar