3.3 - Derivação de Expressões usando Soma de Produtos (SdP)

Tendo por base uma função booleana que possui “n” variáveis ou “n” entradas, consequentemente poderá haver 2ⁿ (dois elevado a n) possibilidades de combinações de valores. Chamamos essas possibilidades de valores que as variáveis podem assumir, juntamente com os respectivos valores da função, de “espaço da função”. A cada combinação de entradas podemos associar um determinado termo produto, no qual todas as variáveis da função estarão presentes, e que é composto da seguinte maneira:

• caso a variável correspondente tiver o valor 0 (zero), ela irá aparecer “negada”;
• se a variável tiver o valor 1 (um), ela deve aparecer como “não negada”.

Veja a tabela abaixo, na qual é possível observar os termos de produto associados a cada combinação de entradas para uma função booleana de três variáveis (A, B, C).

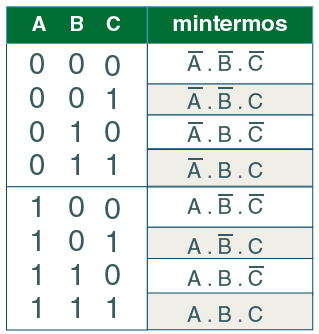Cada termo produto construído conforme a regra falada anteriormente é chamado de mintermo (também pode ser chamado de minitermo). Observe que, para determinado dado mintermo, caso substituirmos os valores das variáveis associadas, obteremos o valor 1 (um). Entretanto, se substituirmos nesse mesmo mintermo por qualquer outra combinação de valores, iremos obter o valor 0 (zero). Dessa maneira, caso queiramos encontrar a equação para uma função tendo por base sua tabela verdade, basta utilizar um “OU” entre os mintermos associados aos números um da função (conhecidos como: mintermos 1).