3.4 - Derivação de Expressões usando Produto de Somas (PdS)

Agora vamos ver que o método de derivação usando produto de somas é o dual (oposto) do método de derivação em soma de produtos. Sendo que em cada combinação das variáveis de entrada de uma função é possível fazer associação a um termo soma, no qual todas as variáveis da função estão presentes e que é formado da seguinte maneira:

• caso uma variável correspondente tenha o valor de 1 (um), ela deve aparecer como: “negada”;
• caso a variável tenha o valor 0 (zero), ela deve aparecer como: “não negada”.

A tabela abaixo faz uma lista dos termos soma associados a cada combinação de entradas para uma função booleana quando utilizamos 3 variáveis (A, B, C).
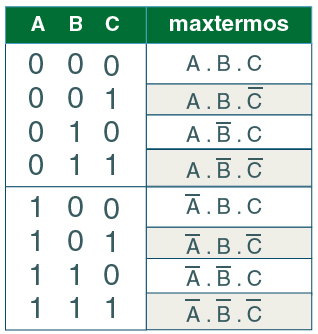Cada termo soma efetuado tendo por base a regra anteriormente falada é chamado de: maxtermo (maxitermo).

Observe que, para um dado maxtermo, caso façamos a subtração dos valores das variáveis associadas, iremos obter o valor “0” (zero). Todavia, caso façamos a substituição nesse mesmo maxtermo com qualquer tipo de combinação de valores, iremos obter o valor 1 (um).

Dessa maneira, caso queiramos encontrar a equação para uma função tendo por base a respectiva tabela verdade, basta utilizar um “E” entre os maxtermos associados aos valores zero da função que também podemos chamar de: maxtermos 0 (zero).




Copyright © 2014 AIEC.