Módulo 01 - Ordenamentos, o Direito e a Moral.

Retornando à função F que utilizamos como exemplo nos parágrafos anteriores, podemos refazer a expressão em soma de produtos, na forma canônica, como o seguinte:

Podemos deixar esta expressão mais enxuta usando o símbolo de somatório (∑); vamos lá:

Uma expressão em produto de somas, na forma canônica, podemos reescrever da seguinte forma:

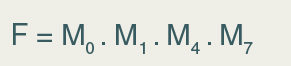
Podemos, também, deixar esta expressão mais enxuta utilizando o símbolo de produto (∏); vamos lá:

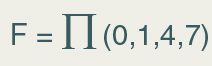
Você deve ter notado que mesmo as representações canônicas sendo práticas, elas são pouco úteis quando o assunto é a implementação de circuitos digitais. O número de portas lógicas e conexões de um circuito lógico depende diretamente do número de operações booleanas (E, inversão, OU) contidas na expressão associada. Sendo assim, é mais prático a redução do número de operações contidas numa função, de tal maneira poder implementar utilizando circuitos lógicos mais simples, e por consequência, de custo mais reduzido.

A diminuição da quantidade de operações é alcançada por meio da eliminação de literais da expressão, utilizando as propriedades da álgebra booleana descritas nos parágrafos anteriores. Podemos dizer que um “literal” pode ser uma “variável negada” ou uma “variável não negada”. Chamamos de simplificação o processo de redução de literais ou de redução de operações, equivalentemente.