Vamos agora usar exemplos para entendermos os passos básicos para a simplificação algébrica (literal) de expressões booleanas. Vamos utilizar uma expressão canônica, em soma de produtos, para uma dada função F:

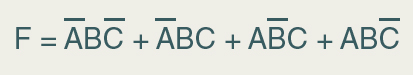
A primeira observação que precisamos fazer é a identificação dos pares de “mintermos” que se diferenciam por apenas um literal, a fim de aplicar a propriedade (14). Os mintermos A C B e ABC , por exemplo, possuem os mesmos literais, exceto pela variável C: no primeiro, o literal é C , enquanto no segundo, o literal é C. Então, conforme a expressão abaixo que exemplifica que a propriedade Distributiva diz “da multiplicação em relação à adição”:

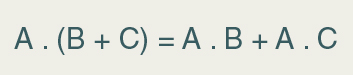
Tendo por base esta propriedade podemos fatorar esses dois mintermos, tendo como resultado a expressão abaixo:

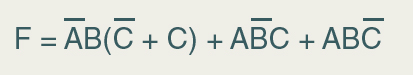
Então pela propriedade Distributiva temos que C + C= 1 . Então, substituindo na expressão acima, obtemos:

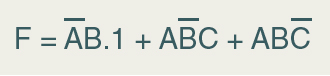
Pela propriedade da multiplicação lógica onde A . 1 = A podemos substituir e obtemos:

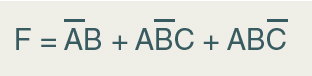
Então, por meio da manipulação algébrica, iremos obter uma expressão em soma de produtos mais enxuta em comparação à mesma expressão em soma de produtos na forma canônica, em virtude da redução do número de operações e também de literais.

Os símbolos utilizados para representar a operação complementação sobre uma variável Booleana A é o “-“ na parte superior da letra, exemplo: Ž.
Observe a equação:

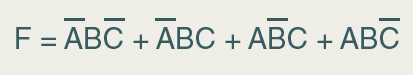
Diferente do que é possível ver na equação acima, poderá haver situações que um mintermo ser . Neste caso ele poderia ser agrupado com o mintermo ABC, pois os dois possuem os mesmos literais, exceto pela variável A (A no primeiro e A no segundo). É muito natural que os passos que foram seguidos seriam os mesmos falados anteriormente. Sendo assim, a equação resultante seria um pouco diferente, mas com a mesma quantidade de operações, sendo, por conseguinte, da mesma complexidade. Realmente, a melhor maneira seria se fosse possível agrupar o mintermo A C B com o mintermo ABC e ao mesmo tempo com o mintermo ABC . Por sorte, a propriedade “Da adição lógica” da álgebra booleana diz que (A + A = A); então o “OU” entre duas ou mais variáveis booleanas iguais é igual a própria variável booleana. Saiba +

Fazendo uma ampliação desta propriedade, podemos falar que o “OU” entre duas ou mais funções (também os produtos) booleanas iguais é equivalente à própria função booleana. Desta maneira, podemos expandir o mintermo para:

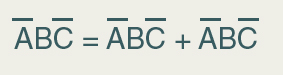
Esta manipulação algébrica é decorrente da propriedade “adição lógica” da álgebra booleana que afirma que (A + A = A).