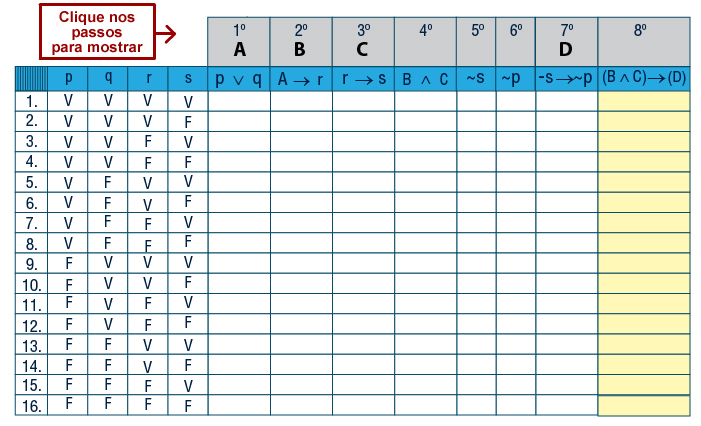
Módulo 01 - Ordenamentos, o Direito e a Moral.

7. Chegamos ao fim da proposição. Note que a operação ainda não abordada foi a seguinte condicional:

((p∨q→r)∧(r→s))→(~s→~p)

8. Ou seja, a resolução final desta tabela verdade será:

(B∧C) → (D)

Agora reveja todos os 8 passos na tabela verdade abaixo.

1º
Como dentro do parêntese há mais de duas operações, aplicamos a precedência para identificar a ordem:

((p ∨ q → r) ∧ (r → s)) → (~s → ~p)

Primeiro será p ? q, que representaremos pela letra maiúscula A, para economizar espaço na tabela na posteriormente.

2º
Depois de p ? q, será a coluna A → r para completar o primeiro parêntese (p ∨ q → r). Para economizar espaço na coluna seguinte, chamaremos de B a coluna A → r.

3º
Resolução do segundo parêntese (r → s). Para economizar espaço na coluna seguinte, chamaremos esta coluna de C, representando a proposição r→s.

4º
Resolução do segundo parêntese ((p ∨ q → r) ∧ (r → s)), que está intitulado como B∧C para economizar espaço da coluna.

5º
Início da resolução do parêntese (~s → ~p). Aplicamos a precedência e resolvemos primeiramente as negações. Neste passo é a resolução de ~s.

6º
Continuidade da resolução do parêntese (~s →~p). Neste passo é a resolução de ~p.

7º
Finalização do parêntese proposição (~s → ~p) com a resolução da condicional → entre as negações. Para economizar espaço adiante, chamamos esta coluna de D.

8º
Resolução da coluna final, que ficou intitulada por (B∧C)→(D), com a utilização das letras maiúsculas nas representações intermediárias na tabela. Esta ultima coluna é a resolução da condicional (B∧C)→(D), pois já se tem as resoluções de (B∧C)e de (D).