Seguindo o mesmo princípio, agora comparando duas proposições que são ambas contradições, então teremos o valor F em todas as linhas de ambos os resultados, eliminando também a possibilidade de ocorrer a combinação V e F simultaneamente.

Veja a seguir um exemplo:

Verificar se

P: ((p∧q)∧~(p∨q)) ⇒ Q: (~p∧(p∧~q))

1º) Tabela verdade de P: (p∧q)∧~(p∨q)

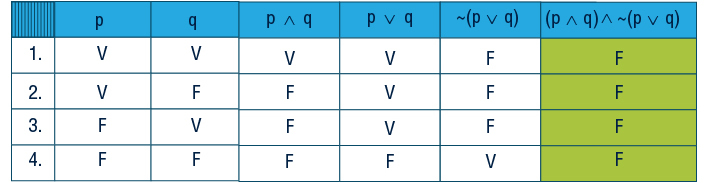
2º) Tabela verdade de Q: ~p∧(p∧~q)

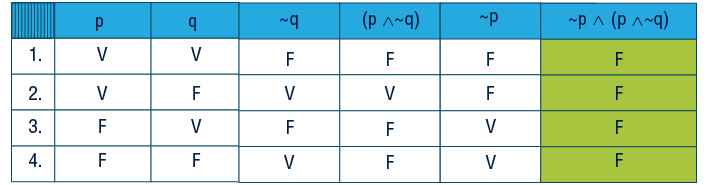
3º) Comparar os resultados das tabelas verdades de P e Q

Comparando os resultados, podemos afirmar que P implica em Q e também que Q implica em P, pois não ocorre “V ⇒ F” simultaneamente na mesma linha.

Conclusão: