São diversas as vantagens de se trabalhar com uma proposição reduzida, tendo a certeza de que a mesma é equivalente à proposição original.
Considere ter que fazer uma tabela verdade de uma proposição. Certamente é menor o trabalho e a possibilidades de erro quando a proposição é pequena. Veja abaixo a complexidade da tabela verdade de (p∧q∧r)∨(p∧~r)∨(p∧~q), que não está totalmente preenchida devido fazer parte do desafio do módulo anterior.
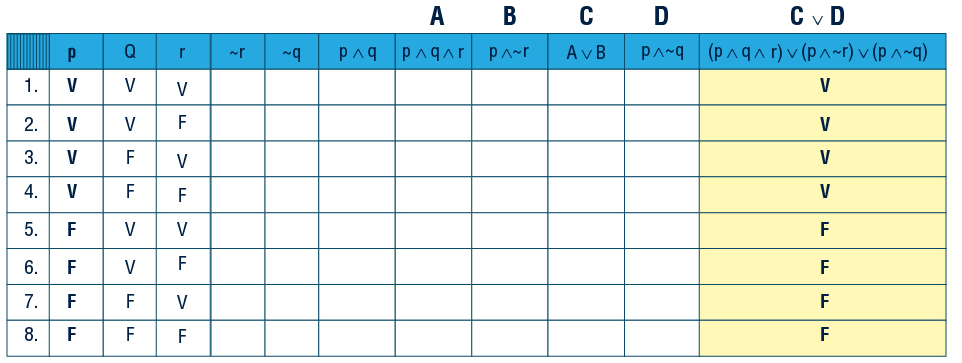
Além disso, mais à frente, na próxima unidade, será também estudada a relação da lógica das proposições com a o projeto de circuitos lógicos, onde a utilização de proposições simplificadas também se apresenta como notória vantagem.
Sendo assim, devemos intensificar o entendimento da aplicação das regras de equivalências notáveis na obtenção de proposições simplificadas.